Práctico 4 Prueba t de Student

Para este capitulo necesitas tener instalado el paquete tidyverse, también ayuda tener el paquete broom. Esta clase del curso puede también ser seguida en este link. Además hay una forma interactiva de esta guía en el siguiente link.

El video de la clase se encuentra disponible en este link.

Puedes encontrar una versión interactiva de esta guía aquí.

La prueba t de student fue desarrollada por Gosset cuando trabajaba para la cervecería Guinness (Student 1908). Esta prueba permite comparar las medias de una muestra con la media teórica de una población, o comparar dos poblaciones. Una de las características de la prueba de student, es que permite la alternativa de ver si dos medias son diferentes o, si uno busca más confianza determinar si una media es mayor, o menor que otra. Para la prueba t de Student, se determina un valor de t, usando la siguiente formula (ecuación (4.1)):

\[\begin{equation} t = \frac{(\bar{x} - \mu)/(\frac{\sigma}{\sqrt{n}})}{s} \tag{4.1} \end{equation}\]

El estadístico \(t\) posee un valor de p asociado dependiendo de los grados de libertad de la prueba.

4.0.1 Pruebas de una muestra

Las pruebas de una muestra nos permiten poner a prueba si la media de una población son distintas a una media teórica. Como ejemplo veremos el caso de las erupciones del géiser Old Faithful, localizado en el Parque Nacional Yellowstone. Un guarda-parque del lugar dice que este géiser erupta cada 1 hora. Por suerte R posee una base de datos de Azzalini and Bowman (1990) llamada faithfull, la cual utilizaremos para determinar si esto es cierto o no usando la función t.test. Esta base de datos tiene dos columnas eruptions, que muestra la duración en minutos de cada erupción y waiting que presenta la espera en minutos entre erupciones.

Cuando usamos esta función con una muestra necesitamos llenar 2 argumentos:

  • x: Un vector con los valores numéricos de a poner a prueba
  • mu: La media teórica a poner a prueba
  • alternative: Puede ser “two.sided”, “less” o “greater”, dependiendo de si uno quiere probar que la muestra posee una media distinta, menor o mayor que la media teórica.

En este caso haríamos lo siguiente

data("faithful")
t.test(x = faithful$waiting, mu = 60, alternative = "two.sided")
## 
##  One Sample t-test
## 
## data:  faithful$waiting
## t = 13.22, df = 271, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 60
## 95 percent confidence interval:
##  69.27418 72.51994
## sample estimates:
## mean of x 
##  70.89706

En este caso el valor de p nos dice que la media es diferente a 60.

4.0.1.1 Ejercicio 1

La base de datos airquality (incorporada como ejemplo en R), muestra entre otras variables las partículas de ozono en Nueva York, cada día de Mayo a Septiembre de 1973 entre las 13:00 y las 15:00 (Chambers et al. 1983). Supongamos que ustedes están a cargo de una agencia ambiental, y están estudiando en que meses deben reducir la actividad vehicular de Nueva York. Para esto planean disminuir a la mitad los pasajes del metro de Nueva York todos los meses que en promedio tengan sobre 55 ppb. Para esto deben comprobar estadisticamente que el mes en que harán esto tiene promedios sobre 55.

4.0.2 Pruebas de dos muestras

Las pruebas de dos muestras nos permiten ver si hay diferencias significativas entre las medias de dos muestras. En la base de datos mtcars, hay una columna que determina si los vehículos son de cambios manuales o automáticos. En este caso 0 significa automático y 1 significa manual. En la figura 4.1 podemos ver una inspección gráfica de las posibles diferencias.

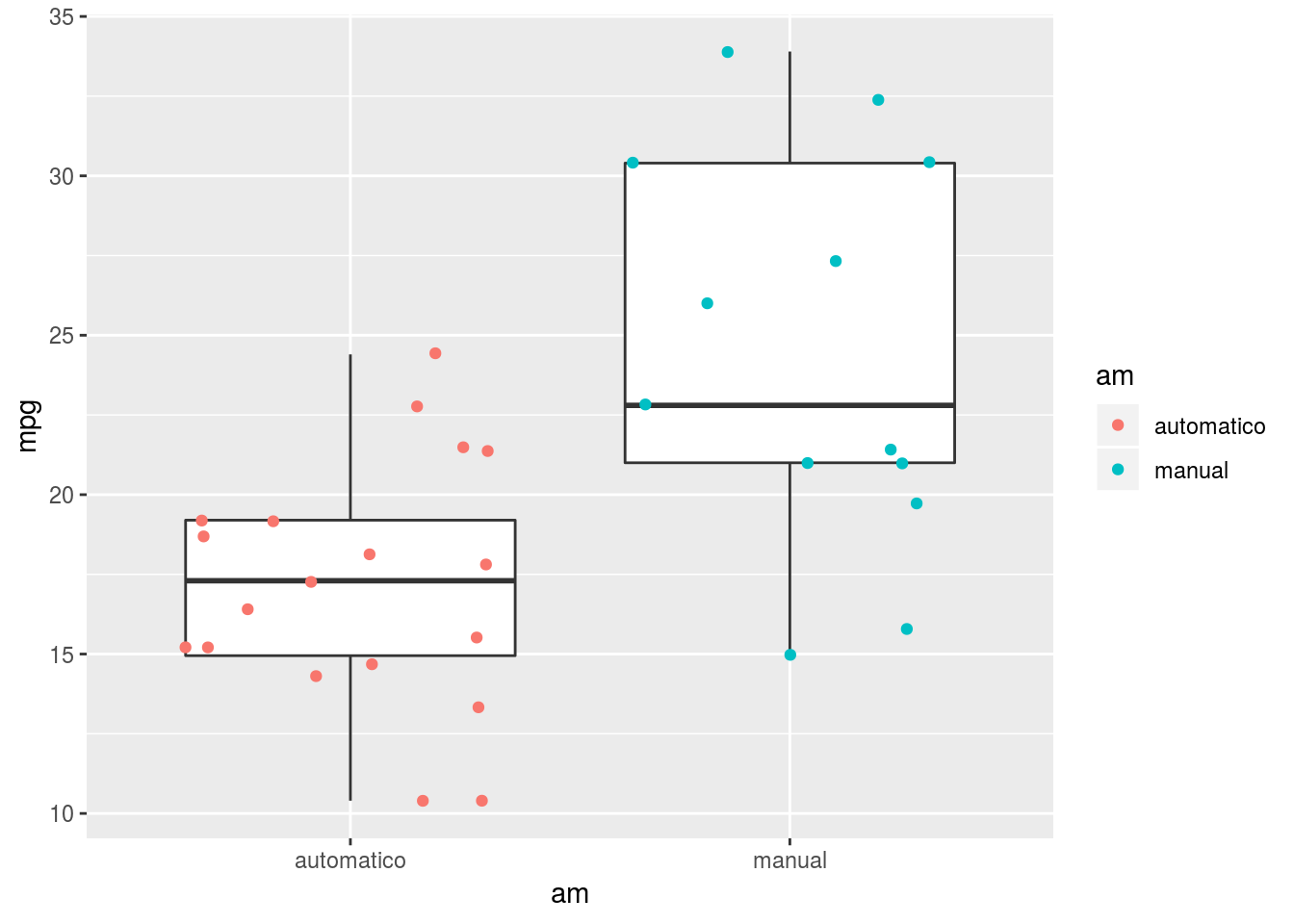
Comparación de eficiencia entre vehiculos automaticos y manuales

Figura 4.1: Comparación de eficiencia entre vehiculos automaticos y manuales

Para hacer la comparación debemos agregar el argumento var.equal el cual en este caso asumiremos que es verdad, ya que en la próxima sección veremos los supuestos de la prueba t y las consecuencias de las violaciones de estos supuestos. En este caso podemos usar el símbolo ~ a ser leído como explicado por para la prueba t de dos muestras.

t.test(mpg ~ am, data = mtcars, var.equal =TRUE)
## 
##  Two Sample t-test
## 
## data:  mpg by am
## t = -4.1061, df = 30, p-value = 0.000285
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -10.84837  -3.64151
## sample estimates:
## mean in group 0 mean in group 1 
##        17.14737        24.39231

En este caso se determinaría que los vehículos manuales (am = 1), son más eficientes que sus contra-partes automáticas.

4.0.2.1 Ejercicio 2

Para el siguiente ejercicio usaremos la base de datos BeerDark disponible en webcursos o en el siguiente link. Esta base de datos posee 7 columnas, pero usaremos solo 4 de ellas:

  • Estilo: Separa las cervezas entre Porters y Stouts
  • Grado_Alcoholico: El grado alcohólico de las cervezas
  • Amargor: Valor IBU (International Bittering Units), a mayor valor más amarga la cerveza
  • Color: A mayor valor más oscura la cerveza.

Determinar si las cervezas Porter y Stouts son distintas en grado alcohólico, amargor y/o color.

4.1 Supuestos de la prueba de t y alternativas

Los supuestos de la t de student son las siguientes (Boneau 1960)

  • Independencia de las observaciones
  • Distribución normal de los datos en cada grupo
  • Homogeneidad de varianza

4.1.1 Prueba de una muestra

Como siempre la independencia de las muestras es algo que solo puede determinarse en base a el diseño del muestreo, y por otro lado, al haber solo una muestra, la homogeneidad de varianza no es un problema, en este caso solo podemos ver si la distribución es normal. Volviendo a nuestro ejemplo de una muestra, con la base de datos faithfull, veamos en base a un histograma (figura 4.2), qqplot (figura 4.3) y test de shapiro, si los datos son normales o no:

hist(faithful$waiting, xlab = "Minutos de espera entre erupciones")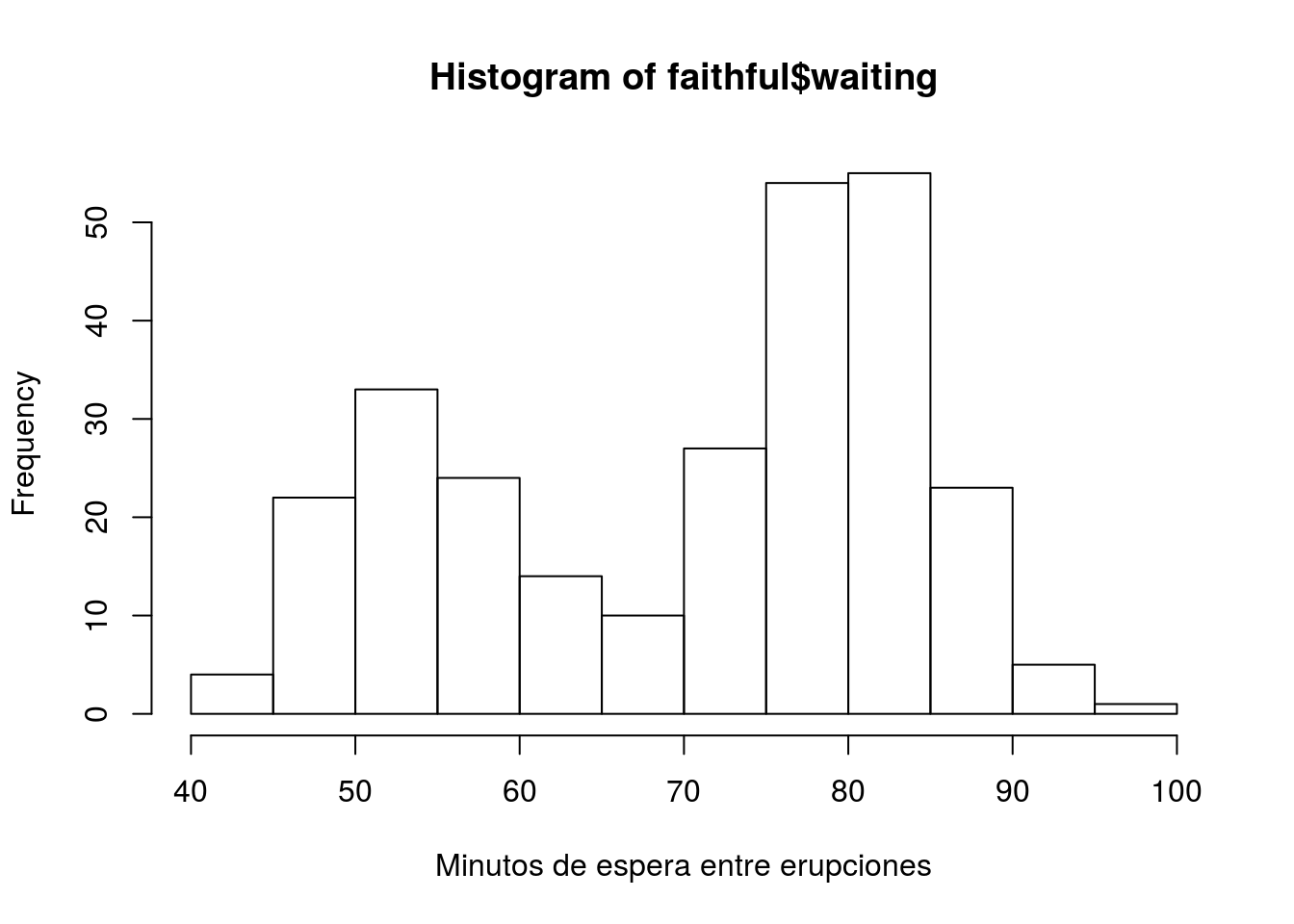
Histograma de los minutos de espera de el géiser Old Fiathful

Figura 4.2: Histograma de los minutos de espera de el géiser Old Fiathful 

qqnorm(faithful$waiting)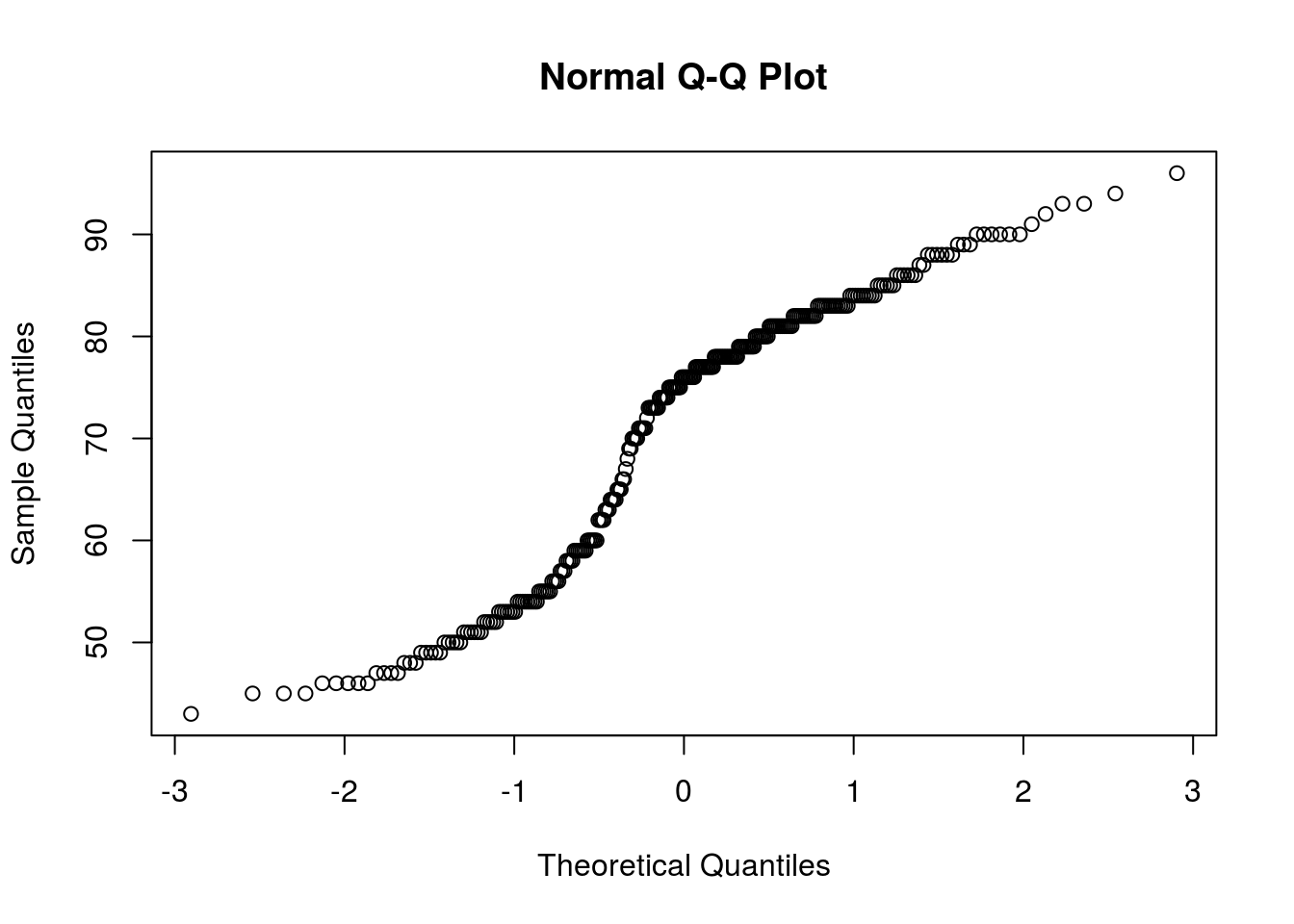
QQplot de los minutos de espera de el géiser Old Fiathful

Figura 4.3: QQplot de los minutos de espera de el géiser Old Fiathful 

shapiro.test(faithful$waiting)
## 
##  Shapiro-Wilk normality test
## 
## data:  faithful$waiting
## W = 0.92215, p-value = 1.015e-10

Como vemos en la figura 2, los datos no se ven normales, incluso se ven bimodales, lo cual significa que tiene 2 picos, en este caso uno al rededor de los 52 minutos y otro al rededor de los 85 minutos de espera (recordemos que la función hist, automáticamente usa el algoritmo de Sturges (1926), para determinar como dividir los datos y obtener el mejor histograma). Nuestras sospechas de no normalidad son confirmadas al ver el qqplot, que no sigue para nada la diagonal, y es reafirmado por el test de shapiro, cuyo valor mucho menor a 0.05, nos dice que la distribución no es normal. Dado esto, debemos apelar a un test de distribución libre como el de Mann-Whitney, la cual se realiza con la función wilcox.test, de la misma forma que es utilizada la función t.test, por lo tanto para nuestro ejemplo usamos:

data("faithful")
wilcox.test(x = faithful$waiting, mu = 60, alternative = "two.sided")
## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  faithful$waiting
## V = 31048, p-value < 2.2e-16
## alternative hypothesis: true location is not equal to 60

Que en este caso nos lleva a la misma conclusión que nuestro ejemplo anterior.

4.1.2 Prueba de dos muestras

Para una prueba de dos muestras, podemos testear tanto la homogeneidad de varianza como la normalidad, para ver las dos cosas al mismo tiempo podemos usar un gráfico de violín (figura 4.4). En este caso, las distribuciones no se ven muy diferentes a la normalidad, pero las varianzas se ven un tanto distintas, podemos seguir explorando esto visualmente usando la función hist previamente generando dos data frames, uno para autos automático y otro para manuales.

data("mtcars")
mt <- mtcars
mt$am <- ifelse(mtcars$am  == 0, "automatico", "manual")
mt <- as.data.frame(mt)
ggplot(mt, aes(x = am, y = mpg)) + geom_violin()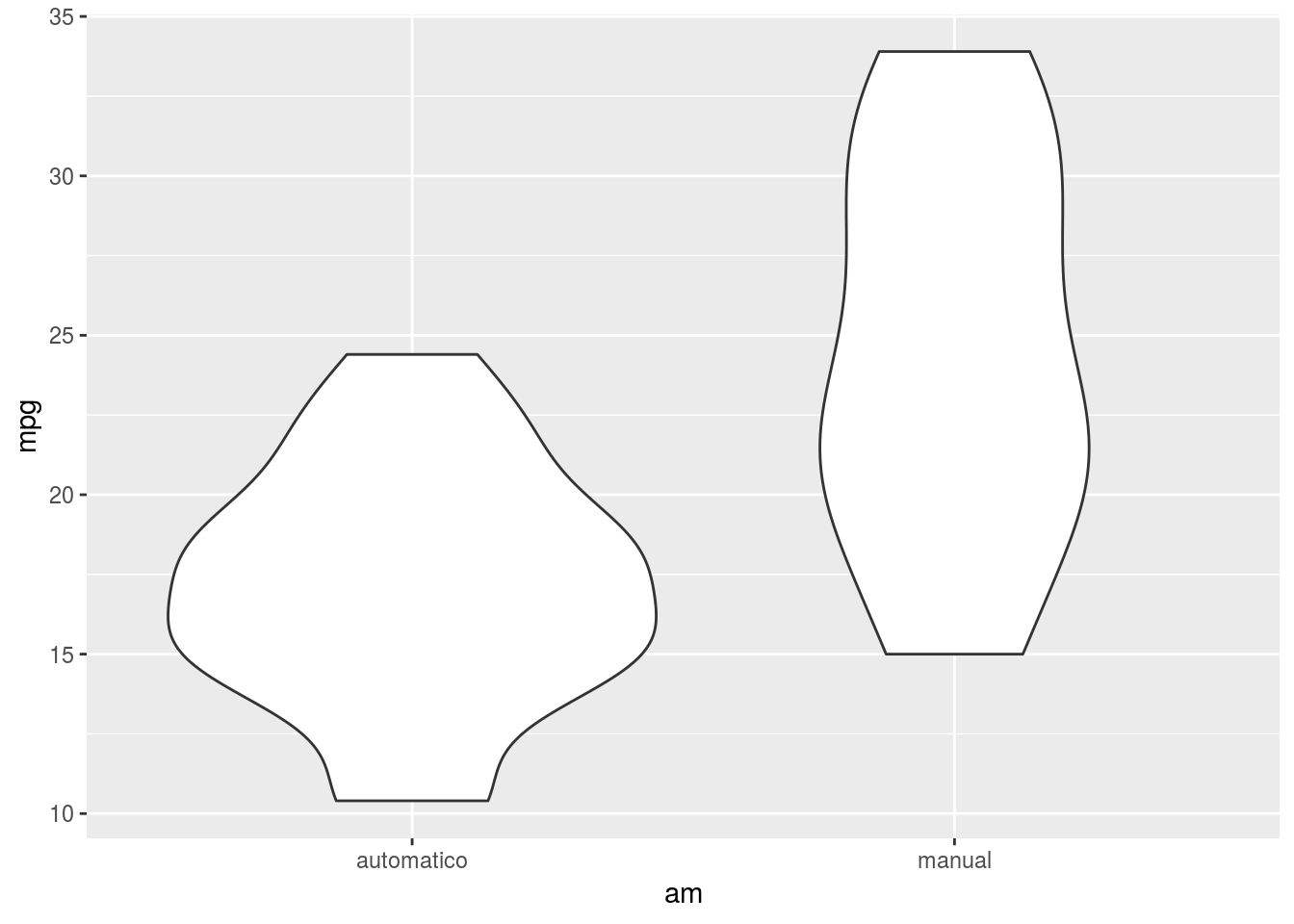
Comparación de distribuciones y varianzas de los vehiculos automáticos

Figura 4.4: Comparación de distribuciones y varianzas de los vehiculos automáticos

En este caso, las distribuciones no se ven muy diferentes a la normalidad, pero las varianzas se ven un tanto distintas, podemos seguir explorando esto separando los datos en vehículos automáticos y manuales para hacer histogramas, en este caso es importante que los ejes sean iguales, para eso en el histograma usaremos los parámetros ylim y xlim.

hist(manuales$mpg, xlim = c(10,35), ylim = c(0,5))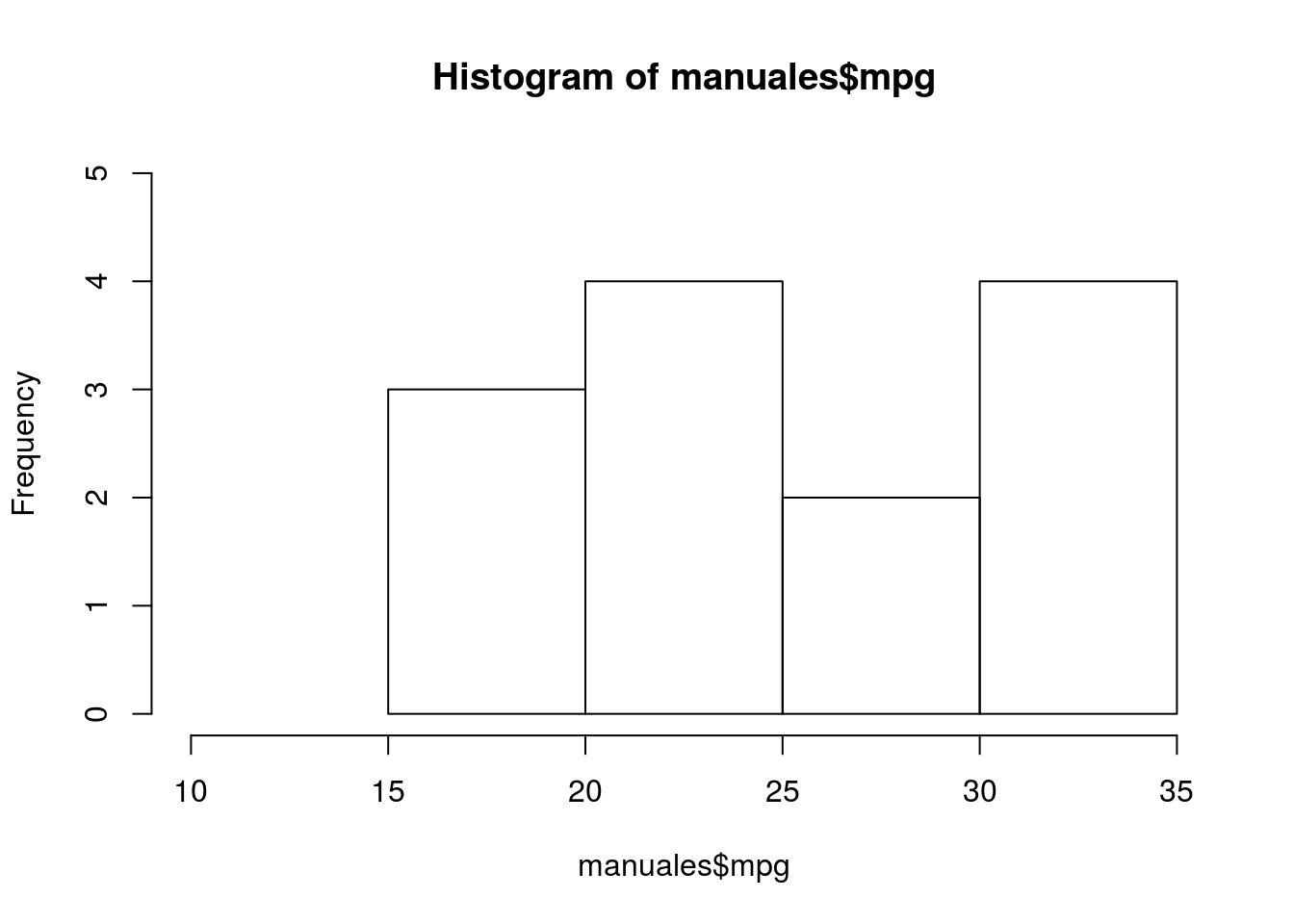
Histograma de vehiculos manuales

Figura 4.5: Histograma de vehiculos manuales 

hist(autos$mpg, xlim = c(10,35), ylim = c(0,5))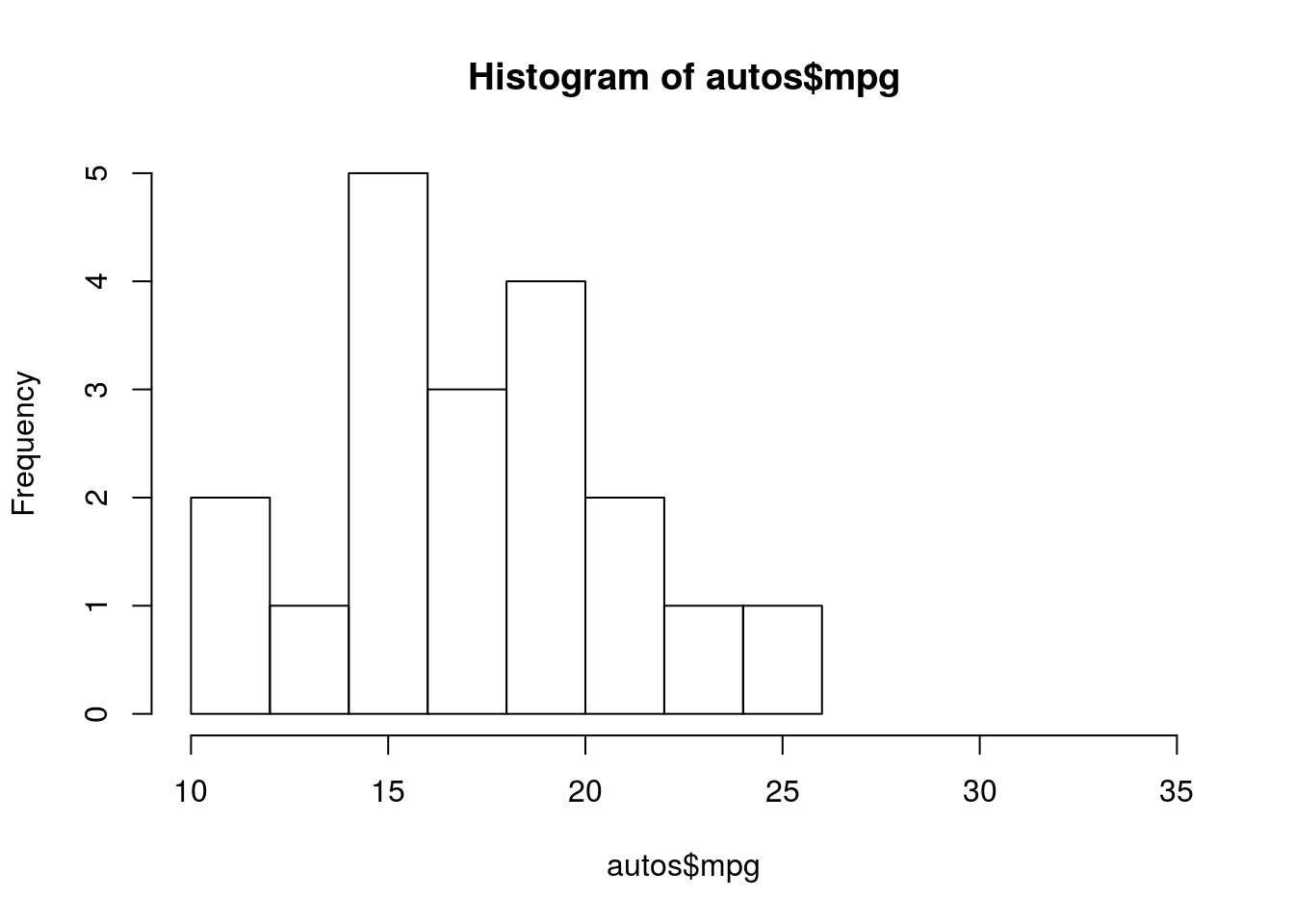
Histograma de vehiculos automáticos

Figura 4.6: Histograma de vehiculos automáticos

Como vemos, los vehículos manuales no parecen tener distribución normal como se ve en la figura 4.5, esto podemos comprobarlo con el qqlot de los mismos datos (figura 4.7)

qqnorm(manuales$mpg)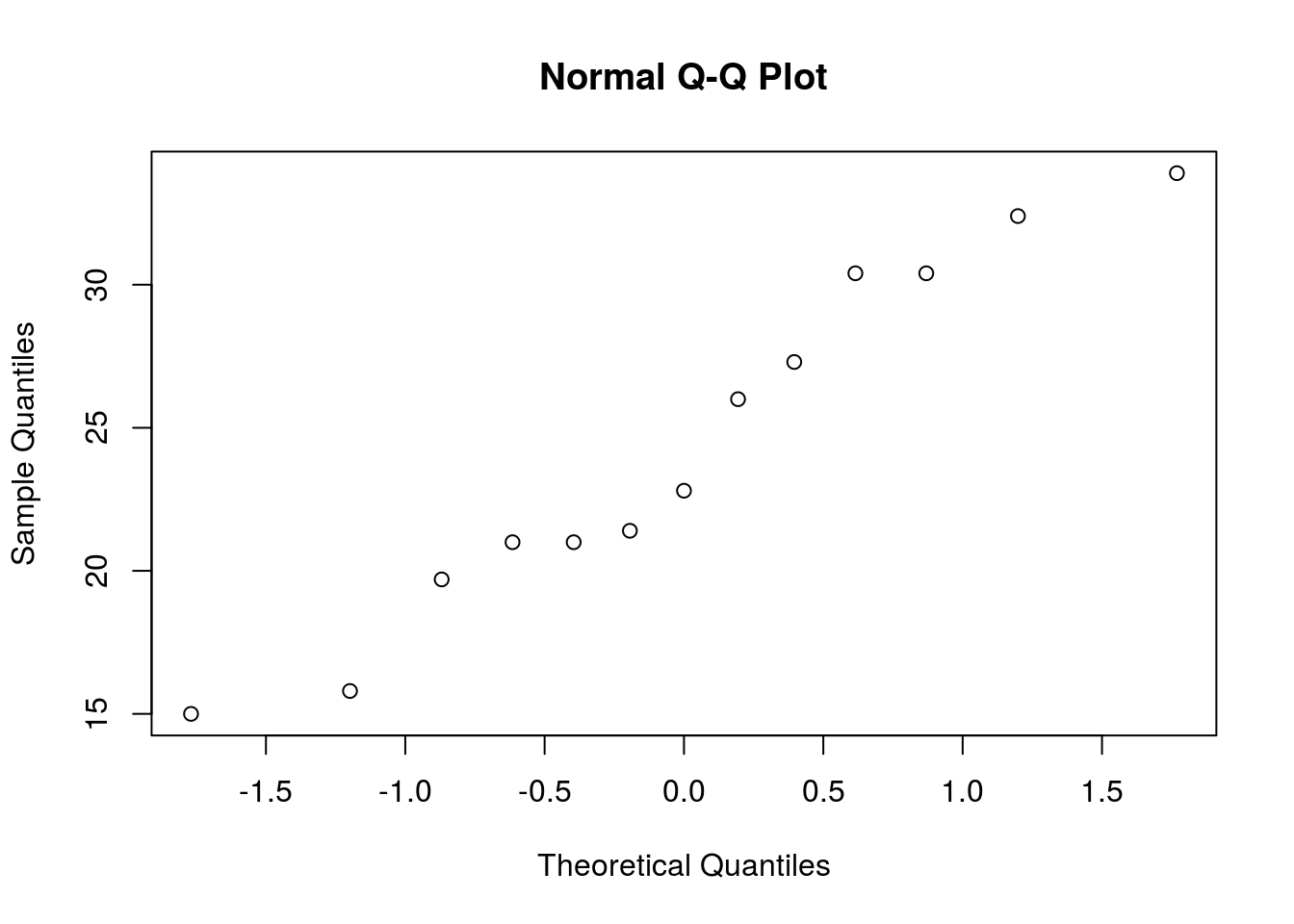
QQplot de eficiencia de vehiculos con cambios manuales

Figura 4.7: QQplot de eficiencia de vehiculos con cambios manuales

4.1.2.1 Ejercicio 3

Como siempre la independencia de las muestras es algo que solo puede determinarse en base a el diseño del muestreo, y por otro lado, al haber solo una muestra, la homogeneidad de varianza no es un problema, en este caso solo podemos ver si la distribución es normal. Volviendo a nuestro ejercicio de una muestra, con la base de datos airquality, evalúe basado en histograma, qqplot y test de shapiro si se debe revaluar la hipótesis para los meses de julio y agosto

Para una prueba de dos muestras, podemos testear tanto la homogeneidad de varianza como la normalidad, para ver las dos cosas al mismo tiempo podemos usar un gráfico de violín geom_violin en ggplot2, lo cual puede seguir siendo explorando esto visualmente usando la función hist generando dos data frames, uno por cada clase de datos.

Evalúe si es necesario revaluar la hipótesis de que el amargor es distinto entre ambos estilos de cerveza

4.2 Bibliografía

Referencias

Student. 1908. “The Probable Error of a Mean.” Biometrika. JSTOR, 1–25.

Azzalini, Adelchi, and Adrian W Bowman. 1990. “A Look at Some Data on the Old Faithful Geyser.” Applied Statistics. JSTOR, 357–65.

Chambers, John M, William S Cleveland, Beat Kleiner, and Paul A Tukey. 1983. “Graphical Methods for Data Analysis. 1983.” Wadsworth, Belmont, CA 35.

Boneau, C Alan. 1960. “The Effects of Violations of Assumptions Underlying the T Test.” Psychological Bulletin 57 (1). American Psychological Association: 49.

Sturges, Herbert A. 1926. “The Choice of a Class Interval.” Journal of the American Statistical Association 21 (153): 65–66.