Práctico 1 Exploración de datos y tu primer ANOVA

1.1 Paquetes necesarios para este práctico

Para este capitulo necesitas tener instalado el paquete tidyverse. Esta clase del curso puede también ser seguida en este link. El video de la clase se encuentra disponible en este link.

1.2 Actividad 1 Educación en Chile

En esta actividad exploraremos los resultados de la PSU en Chile para el año 2017. Pueden encontrar la base de datos original en Data Chile.

Trataremos de determinar, usando el puntaje de la PSU como medida, si existen brechas en la educación chilena por tipo de institución. Para ello, primero trabajaremos realizando análisis exploratorios en base a gráficos y tablas resumen usando funciones del paquete tidyverse (Wickham 2017) en R.

La base de datos EducacionChile.csv se encuentra disponible en webcursos o en https://es.datachile.io/geo/chile#education.

1.2.1 Tablas resumen de los datos:

Lo primero que deben hacer es generar una tabla resumen usando el tidyverse usando las funciones group_by para agrupar por variables y summarize para resumir los datos, dentro de summarize podemos usar variables como:

  • mean() promedio
  • sd() desviación estándar
  • n() número de muestras

a modo de ejemplo vemos la tabla 1.1 mostrando la media y número de muestras con la base de datos iris:

data("iris")
Table <- group_by(iris, Species) %>% summarize(Promedio = mean(Petal.Length), N = n())
knitr::kable(Table)
Tabla 1.1: Resumen con la media y número de muestras del largo de pétalo de las flores de tres especies del género Iris
Species Promedio N
setosa 1.462 50
versicolor 4.260 50
virginica 5.552 50

Basado en el resumen ¿Qué podemos decir de estos datos de educación en Chile?

1.2.2 Visualización de datos con ggplot2 (tidyverse)

El paquete ggplot2 (Wickham 2016) es una poderosa herramienta para graficar datos. Si desean ahondar en el uso de este paquete, pueden ver el siguiente link http://zevross.com/blog/2014/08/04/beautiful-plotting-in-r-a-ggplot2-cheatsheet-3/. En este caso, aprenderemos a graficar boxplots y jitterplots, dos opciones para visualizar una variable categórica versus una cuantitativa.

1.2.2.1 Uso del ggplot2

Su función principal es ggplot, luego de cada función usaremos el símbolo + como usábamos el pipeline (%>%).

Primero usamos la función ggplot para determinar la base de datos y variables, acá las variables siempre van dentro de la función aes

ggplot(MiBaseDeDatos, aes(x = VariableX, y = VariableY))

Luego agregamos el tipo de gráfico que queremos para nuestra figura usando el + como pipeline

ggplot(MiBaseDeDatos, aes(x = VariableX, y = VariableY)) + geom_boxplot()

1.2.2.2 Ejemplo usando la base de datos iris

1.2.2.2.1 Boxplot

El siguiente código muestra como graficar un boxplot para la base de datos iris, la cual esta en R. En este caso graficaremos el largo del pétalo para cada especie (Figura 1.1).

data("iris")
ggplot(iris, aes(x = Species, y = Petal.Length)) + geom_boxplot()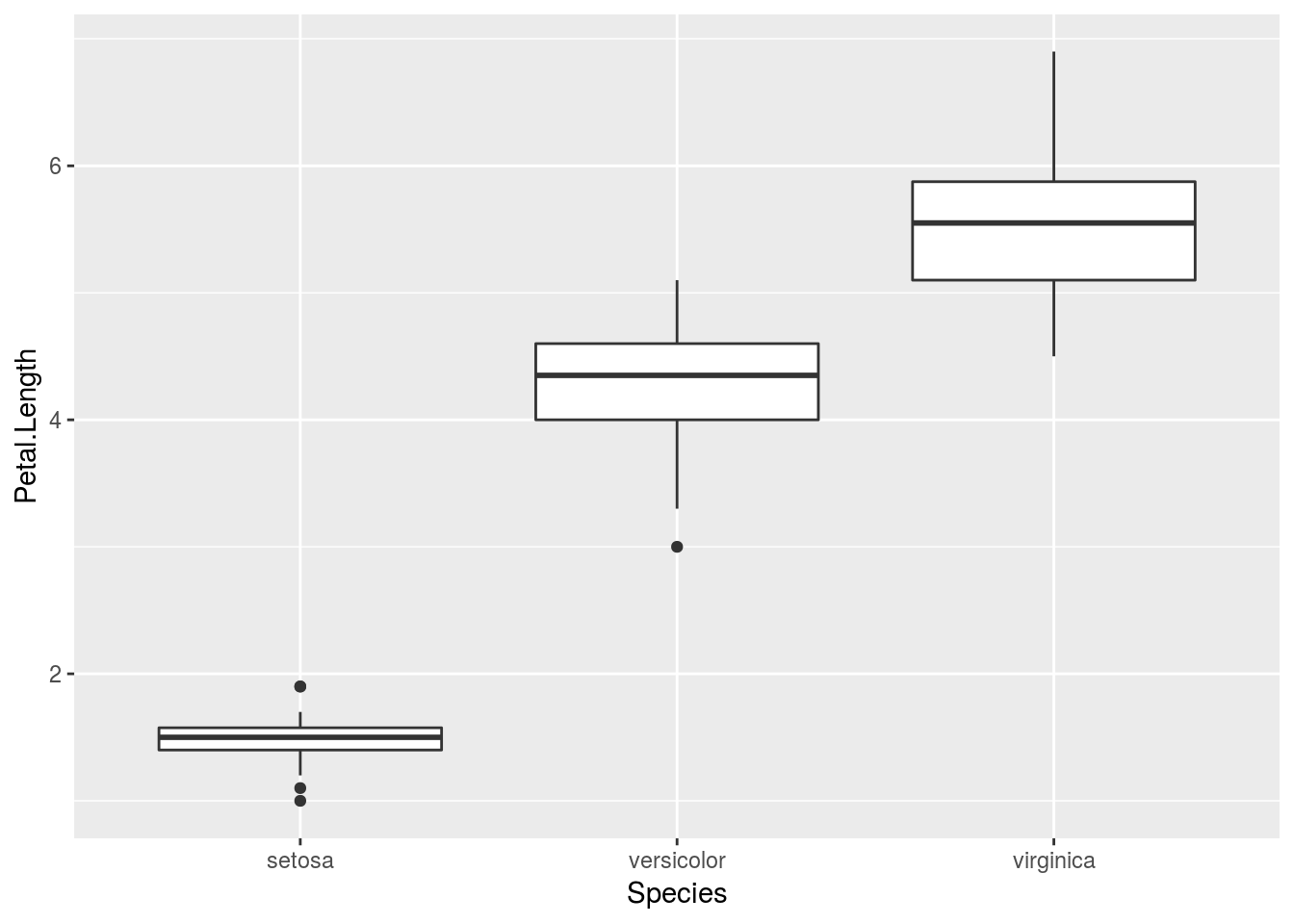
Box plot del largo de petalo de tres especies del género Iris

Figura 1.1: Box plot del largo de petalo de tres especies del género Iris

En los Box Plots tenemos 4 visualizaciones:

  • Mediana (linea gruesa)
  • Caja (Cuantiles 25% y 75%)
  • Bigotes (intervalo de confianza del 95%)
  • Puntos Outlayers

Realice un boxplot de los datos de la educación de Chile, ¿Qué nos dice esto de los datos?

1.2.2.2.2 Jitter plot

El jitter plot suma un punto por cada observación, lo cual nos permite entender un poco más la naturaleza de los datos. En general se le agrega a un box plot para tener mayor claridad en los datos (Figura 1.2).

data("iris")
ggplot(iris, aes(x = Species, y = Petal.Length)) + geom_boxplot() + geom_jitter(aes(color = Species))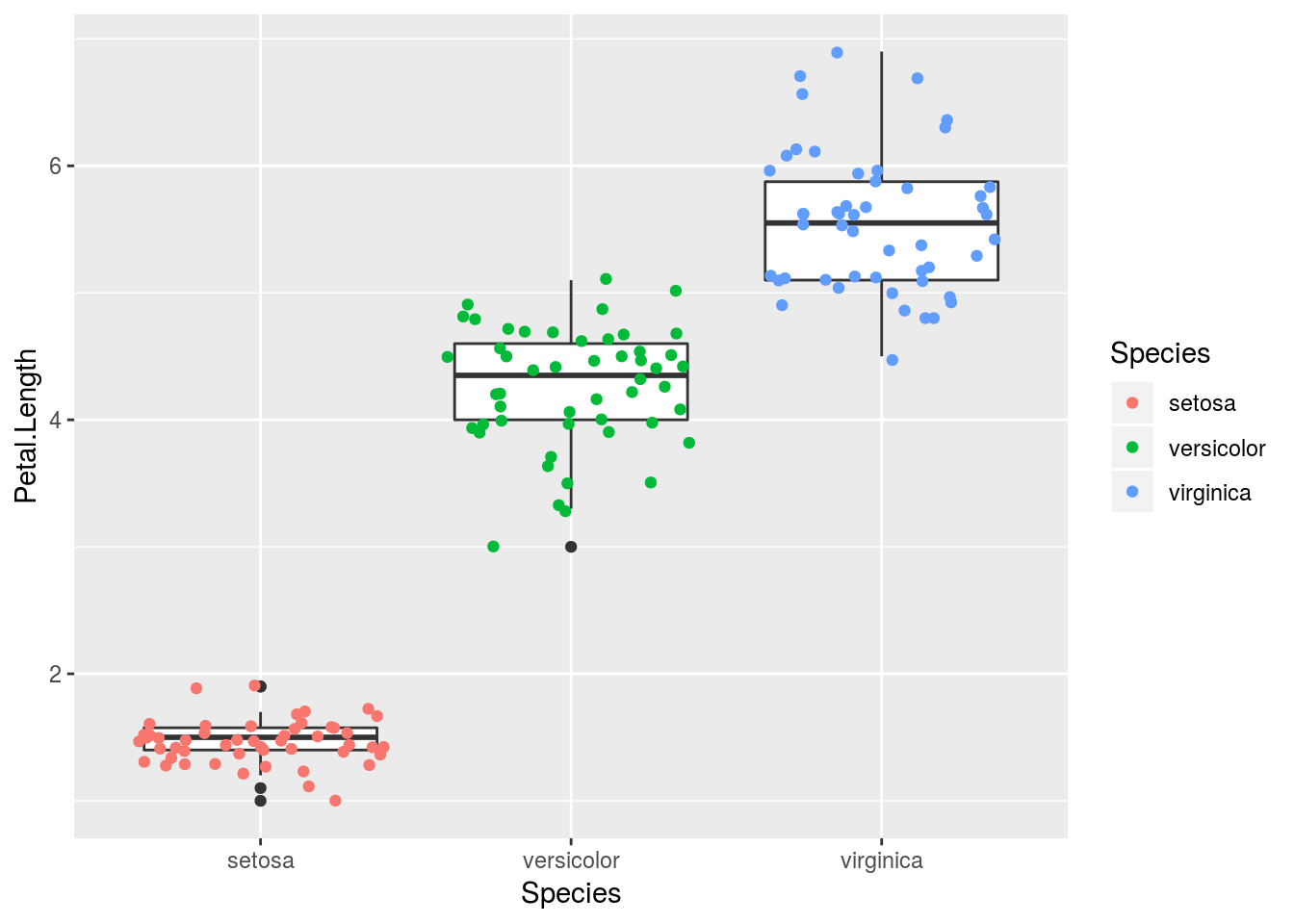
Box plot y jitter plot juntos para el largo de petalo de tres especies del género Iris

Figura 1.2: Box plot y jitter plot juntos para el largo de petalo de tres especies del género Iris

1.3 Actividad 2 Captación de CO2 en plantas

Utilizaremos base de datos \(CO_2\) (Potvin, Lechowicz, and Tardif 1990) enviada al curso. Esta base de datos, también presente en R, tiene las siguientes variables

  • Plant: Identidad de cada planta
  • Type: Variedad de la planta (subespecie Quebec o Mississippi)
  • Treatment: Tratamiento de la planta, algunas fueron enfriadas la noche anterior (Chilled)
  • conc: Concentración ambiental de \(CO_2\)
  • Uptake: Captación de \(CO_2\) para cada planta en cada día

¿Hay diferencias entre la captación de \(CO_2\) en plantas tratadas y no tratadas?

  • Genere tablas resumenes que le permitan explorar esta pregunta
    • ¿Existen variables que puedan confundir el resultado? ¿como trataría los datos para lidiar con esto?
  • Genere gráficos exploratorios para contestar esta pregunta

1.4 Actividad 3 Mi primer ANOVA

1.4.1 antes de empezar a entender el ANOVA

El ANOVA compara medias entre grupos, lo principal es la comparación entre los cuadrados de los residuales intergrupos, y los residuales intragrupos, los primeros son los cuadrados de la diferencia entre las medias de todas las observaciones (\(\tilde{x}_t\)) y las medias de cada grupo \(\tilde{x}_g\) al cuadrado multiplicado por el número de observaciones totales (ver ecuación (1.1)), cambia las medias del simlador de anova a continuacion y selecciona los errores intergrupos y ve como cambian.

\[\begin{equation} \textrm{Errores_inter_factor} = n \times \sum{(\tilde{x}_t - \tilde{x}_g)^2} \tag{1.1} \end{equation}\]

los residuales intra grupos son la diferencia entre cada observación \(x_{i,g}\) del grupo \(g\) y las medias del grupo respectivo (ver ecuación (1.2)), cambia las medias del simlador de anova a continuacion y selecciona los errores intragrupos y ve como cambian

\[\begin{equation} \textrm{Errores_intra_factor} = \sum{(\tilde{x}_g - x_{i,g})^2} \tag{1.2} \end{equation}\]

1.4.1.1 Simulador de ANOVA

1.4.2 Como hacer un ANOVA en R

En R todos los modelos tienen la siguiente estructura Funcion(y ~ x1 + x2 + … + xn, data = MisDatos), donde la Funcion dice el modelo que queremos realizar (por ejemplo ANOVA, regresión lineal, modelos mixtos, etc.), y es la variable que queremos explicar, x1 a xn son las variables explicativas, ~ es un símbolo que debe ser leído como explicado por y finalmente data es la base de datos que queremos utilizar, en un ANOVA (análisis de varianza), la función en cuestión es aov.

En el siguiente código vemos si el largo del pétalo de las flores del género Iris, pueden ser explicados por la especie a la que estas plantas pertenecen, por lo que generamos un modelo llamado Primer.Anova con la función aov.

Primer.Anova <- aov(Petal.Length ~ Species, data = iris)

Para acceder a la tabla de resultados utilizamos la función summary

##              Df Sum Sq Mean Sq F value Pr(>F)    
## Species       2  437.1  218.55    1180 <2e-16 ***
## Residuals   147   27.2    0.19                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Si establecemos el valor de alfa en 0.05 y al ver en la tabla que el valor de p es menor a alfa, rechazamos la hipótesis nula de que las medias son iguales, y decidimos que la media del largo de pétalo es distinta entre las especies.

1.4.3 Ejercicio

Determine si para la base de datos CO2 la captación de \(CO_2\) es distinto entre plantas con tratamiento de enfriamiento y sin enfriamiento.

Referencias

Wickham, Hadley. 2017. Tidyverse: Easily Install and Load the ’Tidyverse’. https://CRAN.R-project.org/package=tidyverse.

Wickham, Hadley. 2016. Ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York. http://ggplot2.org.

Potvin, Catherine, Martin J Lechowicz, and Serge Tardif. 1990. “The Statistical Analysis of Ecophysiological Response Curves Obtained from Experiments Involving Repeated Measures.” Ecology 71 (4). Wiley Online Library: 1389–1400.