Práctico 6 Como formular tu ANOVA

Para este capitulo necesitas tener instalado el paquete tidyverse, también ayuda tener el paquete broom. Esta clase del curso puede también ser seguida en este link

6.1 ANOVA(s)

Si bien el ANOVA puede ser pensado como una extensión de una prueba de T de student, es mucho más complejo que eso, existen muchos tipos de anovas y sus combinaciones, tales como:

• ANOVA
• ANOVA factorial o en bloque
• ANOVA anidado o jerarquico
• ANOVA desbalanceado

Tanta es la variedad de ANOVAS que existen muchos libros dedicados exclusivamente a la discusión de este tipo de análisis (Girden 1992)

6.1.1 ANOVA simple

En la versión más senilla del ANOVA, varios grupos comparten una variable que creemos que es diferente entre grupos, como por ejemplo ancho de sepalo puede ser differente entre tres especies de Iris, para analizar esto, usaríamos el siguiente código, lo que muestra diferencias en el ancho de sépalo entre especies, lo cual se aprecia en el gráfico 1.

##              Df Sum Sq Mean Sq F value Pr(>F)    
## Species       2  11.35   5.672   49.16 <2e-16 ***
## Residuals   147  16.96   0.115                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1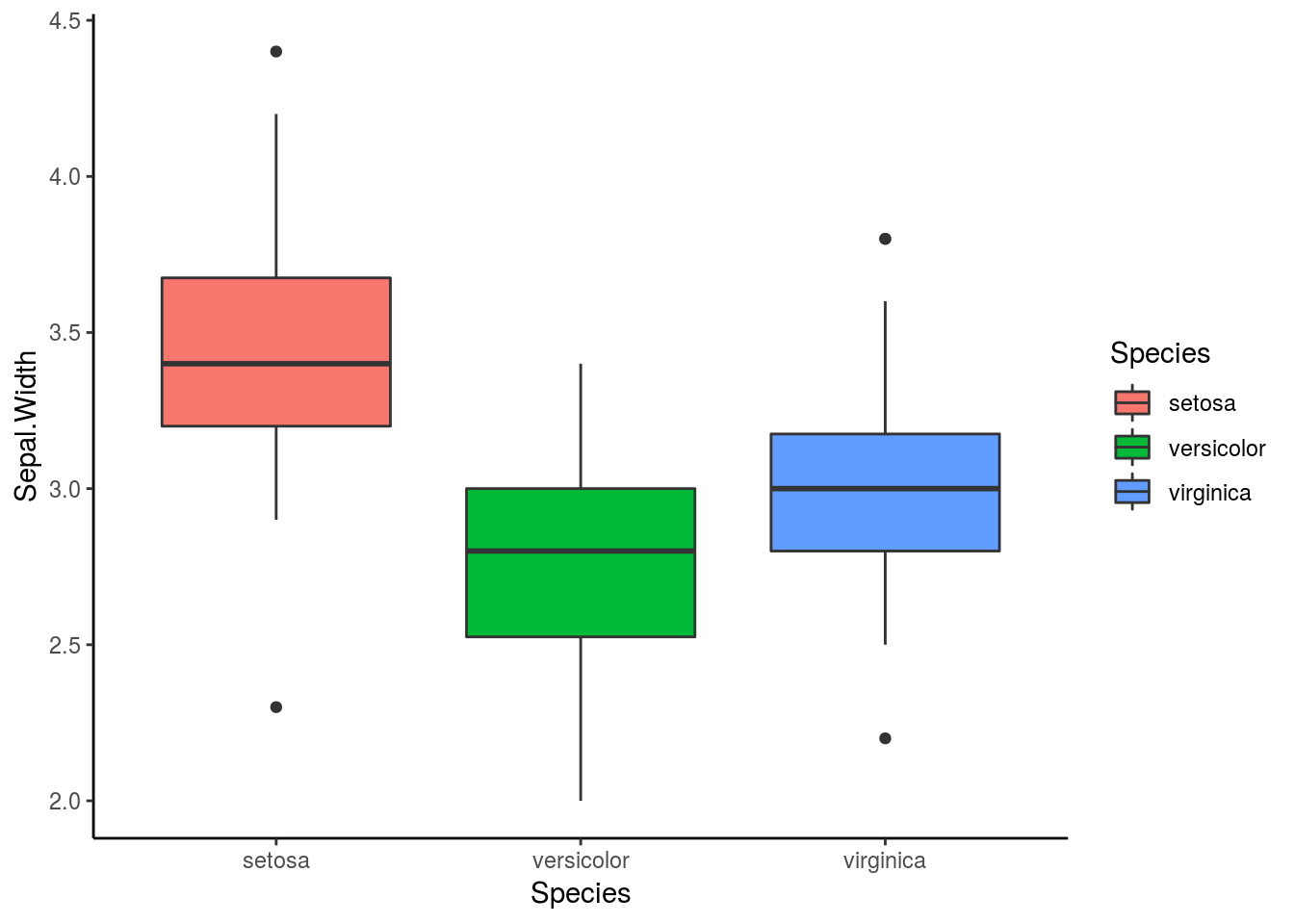

Figura 6.1: Relación entre el ancho del sépalo y las especies de Iris

6.1.2 ANOVA factorial

En el ANOVA factorial, más de un factor puede afectar nuestra variable respuesta. Además, estas variables pueden interactuar, haciendo que el efecto de sobre las muestras sea mas complejo que el efecto de cada variable. Un ejemplo de análisis es la economía de combustible en mtcars según si es automático o manual y el número de cilindros que tiene.

En este caso modificaremos la base de datos para que el factor am en vez de numerico sea factor:

##             Df Sum Sq Mean Sq F value   Pr(>F)    
## am           1  405.2   405.2  46.892 1.93e-07 ***
## cyl          1  449.5   449.5  52.029 7.50e-08 ***
## am:cyl       1   29.4    29.4   3.407   0.0755 .  
## Residuals   28  241.9     8.6                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Aquí vemos que si hay una interacción. Las interacciones las notamos rápidamente en figuras como la que vemos en el grafico 2 imagen B, en la cual cada vez que las lineas no sean paralelas diremos que hay una interacción.

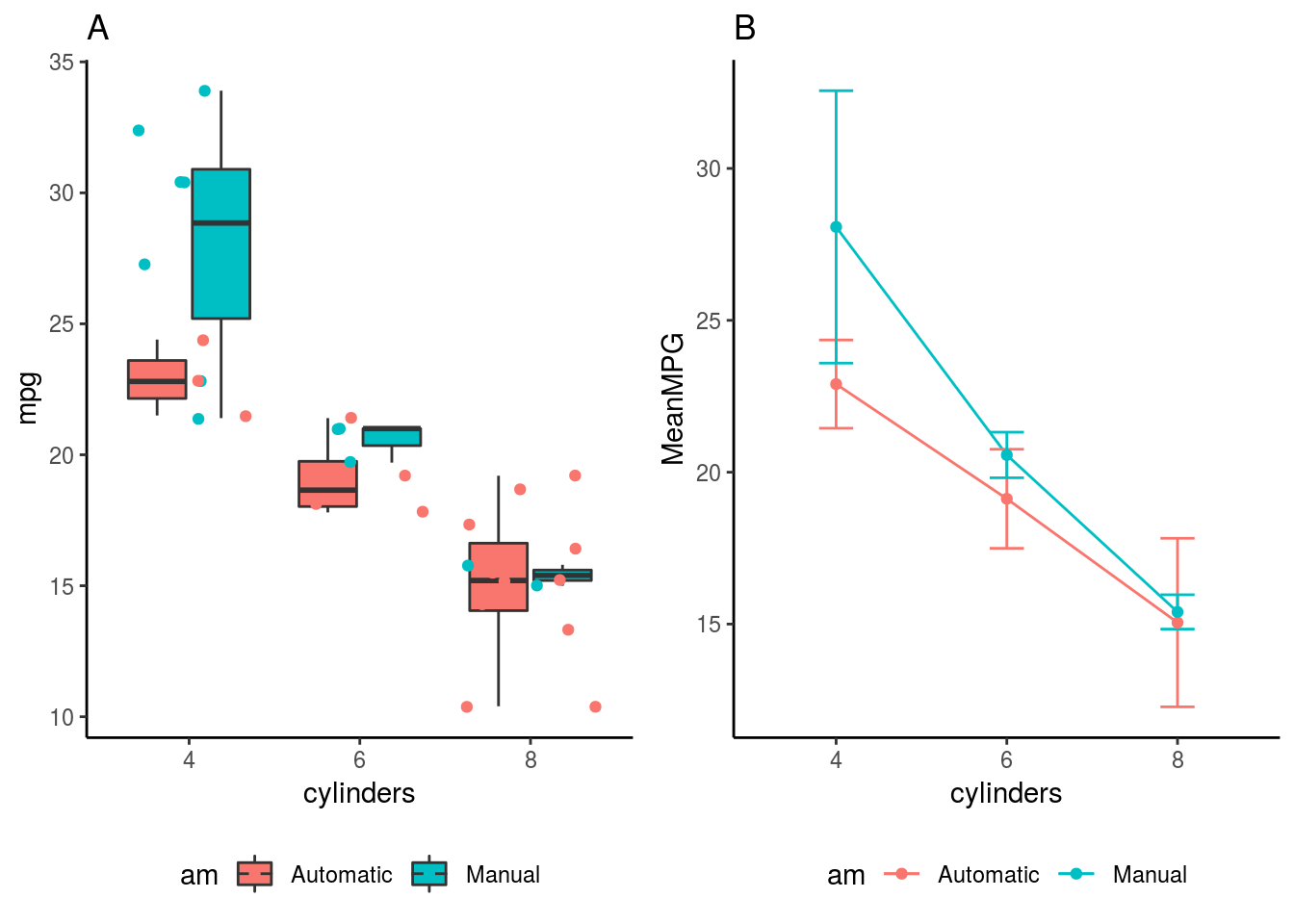
Figura 6.2: Relación entre el número de cilindros, transmición automática o manual, y la economía de combustible de los vehiculos, la relacion la mostramos como un boxplot (A) y como barras de errores unidas por sus medias (B), esta última interpretación permite ver gráficamente las interacciones entre factores

6.1.3 ANOVA anidado o jerarquico

En este tipo de ANOVA tenemos un factor jerarquicamente dentro de otro, por ejemplo individuos dentro de una especie, hojas dentro de un árbol o varias medidas dentro de un mismo individuo. En R dentro de la función aov, si el factor \(B\) esta anidado dentro de \(A\) tenemos A/B como una variable explicativa. Si usamos como ejemplo la de datos CO2, los individuos de cada subespecie estan anidados dentro de cada subespecie. Esto sería analizado con el siguiente codigo:

##                Df Sum Sq Mean Sq F value   Pr(>F)    
## Type            1   3366    3366  50.017 8.13e-10 ***
## Treatment       1    988     988  14.685 0.000269 ***
## Type:Treatment  1    226     226   3.355 0.071152 .  
## Type:Plant      8    283      35   0.525 0.833637    
## Residuals      72   4845      67                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

6.2 Variables fijas vs aleatoreas

En los ANOVA(s), podemos ver dos tipos principales de variables, las cuales son importantes de diferenciar * Variables fijas: Se espera que tengan una influencia predecible y sistemática en sobre lo que queremos explicar. Además usan todos los niveles de un factor (Ejemplo genero) + Uso en R: A + B * Variables aleatorias: Se espera que su influencia sea impredecible e idiosincratica. Además no se usan todos los niveles de un factor (todos los individuos) A + Error(B)

Si volvemos al ejemplo que hemos trabajado ya en clase, en el cual tratamos cada planta como un factor anidado, podemos decir que estas plantas son una variable aleatoria

## 
## Error: Type
##      Df Sum Sq Mean Sq
## Type  1   3366    3366
## 
## Error: Type:Plant
##                Df Sum Sq Mean Sq F value  Pr(>F)    
## Treatment       1  988.1   988.1  27.949 0.00074 ***
## Type:Treatment  1  225.7   225.7   6.385 0.03543 *  
## Residuals       8  282.8    35.4                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Error: Within
##           Df Sum Sq Mean Sq F value Pr(>F)
## Residuals 72   4845   67.29

6.2.1 Más casos y resumen

Trabajaremos con un caso hipotético donde \(Y\) es la variable a explicar y todo el resto (\(A\), \(B\) y \(X\)) son variables explicativas en la base de datos d

6.2.1.1 ANOVA Simple

6.2.1.2 ANOVA con interacciones

Igual a

6.2.1.3 Anovas anidados y otros casos más complejos

• B anidado en A

• A es una variable aleatoria pero B esta anidada en A

• B y X interactuan dentro de niveles aleatorios de A

6.3 Referencias

Referencias

Girden, Ellen R. 1992. ANOVA: Repeated Measures. 84. Sage.