Práctico 5 Comparaciones posthoc y diseños anidados
Para este capitulo necesitas tener instalado el paquete tidyverse, también ayuda tener el paquete broom. Esta clase del curso puede también ser seguida en este link
El video de la clase se encuentra disponible en este link.
5.1 Comparaciones posthoc
Como ya vimos en los prácticos anteriores, un ANOVA sólo puede decirnos si hay diferencias entre grupos, sin embargo no nos dira entre que grupos hay diferencias, es para esto que existen las pruebas posthoc. En el práctico de hoy veremos dos tipos de comparaciones posthoc, la prueba honesta de diferencias significativas de Tukey (función TukeyHSD en R), y los ajustes de valores de p para comparaciones multiples (función pairwise.t.test en R), de las cuales la de Bonferroni es la más habitual.
5.1.1 Prueba honesta de diferencias significativas de Tukey
5.1.1.1 Ejemplo ancho de spealo en el genero Iris
Como vimos en nuestro ejemplo de la guía número 3 (Análisis exploratorio y el primer ANOVA), el ANOVA para determinar si hay diferencias en el ancho de sépalo entre las diferentes especies del genero Iris, son significativas:
summary(aov(Sepal.Width ~ Species, data = iris))## Df Sum Sq Mean Sq F value Pr(>F)
## Species 2 11.35 5.672 49.16 <2e-16 ***
## Residuals 147 16.96 0.115
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Pero este análisis no nos dice en tre que especies encontramos estas diferencias, para esto, podemos realizar una prueba honesta de diferencias significativas de Tukey, para esto utilizamos la función TukeyHSD y usamos como argumento un ANOVA ya ajustado
AnovaSepalo <- aov(Sepal.Width ~ Species, data = iris)
TukeyHSD(AnovaSepalo)## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = Sepal.Width ~ Species, data = iris)
##
## $Species
## diff lwr upr p adj
## versicolor-setosa -0.658 -0.81885528 -0.4971447 0.0000000
## virginica-setosa -0.454 -0.61485528 -0.2931447 0.0000000
## virginica-versicolor 0.204 0.04314472 0.3648553 0.00878025.1.2 Ajustes de valores de p para comparaciones multiples
5.1.2.1 Ajuste de Bonferroni
Cuando realizamos multiples comparaciones pareadas entre grupos, la probabilidad de encontrar diferencias significativas cuando no los hay (error tipo I), aumenta a una tasa dada por la siguiente fórmula:
\[\alpha_{ajustado} = 1 - (1 -\alpha)^n\] Donde \(\alpha\) es la probabilidad de cometer un error tipo I que estamos dispuestos a aceptar (tipicamente 0.05), y \(n\) es el numero de pruebas independientes a realizar.
Con esto según el ajuste de Bonferroni, nuestro p critico para determinar diferencias significativas cambia segun la siguiente fórmula (J. W. Tukey 1977)
\[p-critico_{ajustado} = 1 - (1 -\alpha)^{1/n}\] El ajuste de Bonferroni, sin embargo al disminuir los errores de tipo I, aumenta los errores de tipo II (Morgan 2007). En ese sentido, la función de R pairwise.t.test, nos permite utilizar varios ajustes menos conservadores incluyendo los de Holm (1979), Hochberg (1988), Hommel (1988), Benjamini & Hochberg (1995) o el de Benjamini & Yekutieli (2001)
5.1.2.2 Ejemplo ancho de spealo en el genero Iris
Volviendo al mismo ejemplo que usamos en la prueba de Tukey, mostraremos los valores de p determinados para comparaciones multiples de el ancho de sepalo sin ajuste y con diversos ajustes que encontramos en el la función pairwise.t.test
5.1.2.2.1 Sin ajuste
pairwise.t.test(x = airquality$Ozone, g = airquality$Month, p.adj = "none")##
## Pairwise comparisons using t tests with pooled SD
##
## data: airquality$Ozone and airquality$Month
##
## 5 6 7 8
## 6 0.60877 - - -
## 7 2.9e-05 0.01023 - -
## 8 1.9e-05 0.00831 0.91744 -
## 9 0.32545 0.85838 0.00070 0.00048
##
## P value adjustment method: none5.1.2.2.2 Ajuste de Bonferroni
pairwise.t.test(x = airquality$Ozone, g = airquality$Month, p.adj = "bonf")##
## Pairwise comparisons using t tests with pooled SD
##
## data: airquality$Ozone and airquality$Month
##
## 5 6 7 8
## 6 1.00000 - - -
## 7 0.00029 0.10225 - -
## 8 0.00019 0.08312 1.00000 -
## 9 1.00000 1.00000 0.00697 0.00485
##
## P value adjustment method: bonferroni5.1.2.2.3 Ajuste de Holm
pairwise.t.test(x = airquality$Ozone, g = airquality$Month, p.adj = "holm")##
## Pairwise comparisons using t tests with pooled SD
##
## data: airquality$Ozone and airquality$Month
##
## 5 6 7 8
## 6 1.00000 - - -
## 7 0.00026 0.05113 - -
## 8 0.00019 0.04987 1.00000 -
## 9 1.00000 1.00000 0.00488 0.00388
##
## P value adjustment method: holm5.1.2.2.4 Ajuste de Hommel
pairwise.t.test(x = airquality$Ozone, g = airquality$Month, p.adj = "hommel")##
## Pairwise comparisons using t tests with pooled SD
##
## data: airquality$Ozone and airquality$Month
##
## 5 6 7 8
## 6 0.91744 - - -
## 7 0.00026 0.05113 - -
## 8 0.00018 0.04156 0.91744 -
## 9 0.91744 0.91744 0.00488 0.00339
##
## P value adjustment method: hommel5.1.2.2.5 Diferencias
Se observa como sin ajustar hay 6 pares de meses que tienen diferencias, en contraste con 4 pares de meses con el ajuste de Bonferroni, y 5 con los otros métodos de ajuste de valor de p.
5.2 Diseños anidados
Los diseños anidados ocurren cuando queremos estudiar el efecto de un factor, pero dentro de las muestras existe un segundo factor que puede afectar nuestros análisis, por ejemplo si volvemos a el caso en de la base de datos CO2
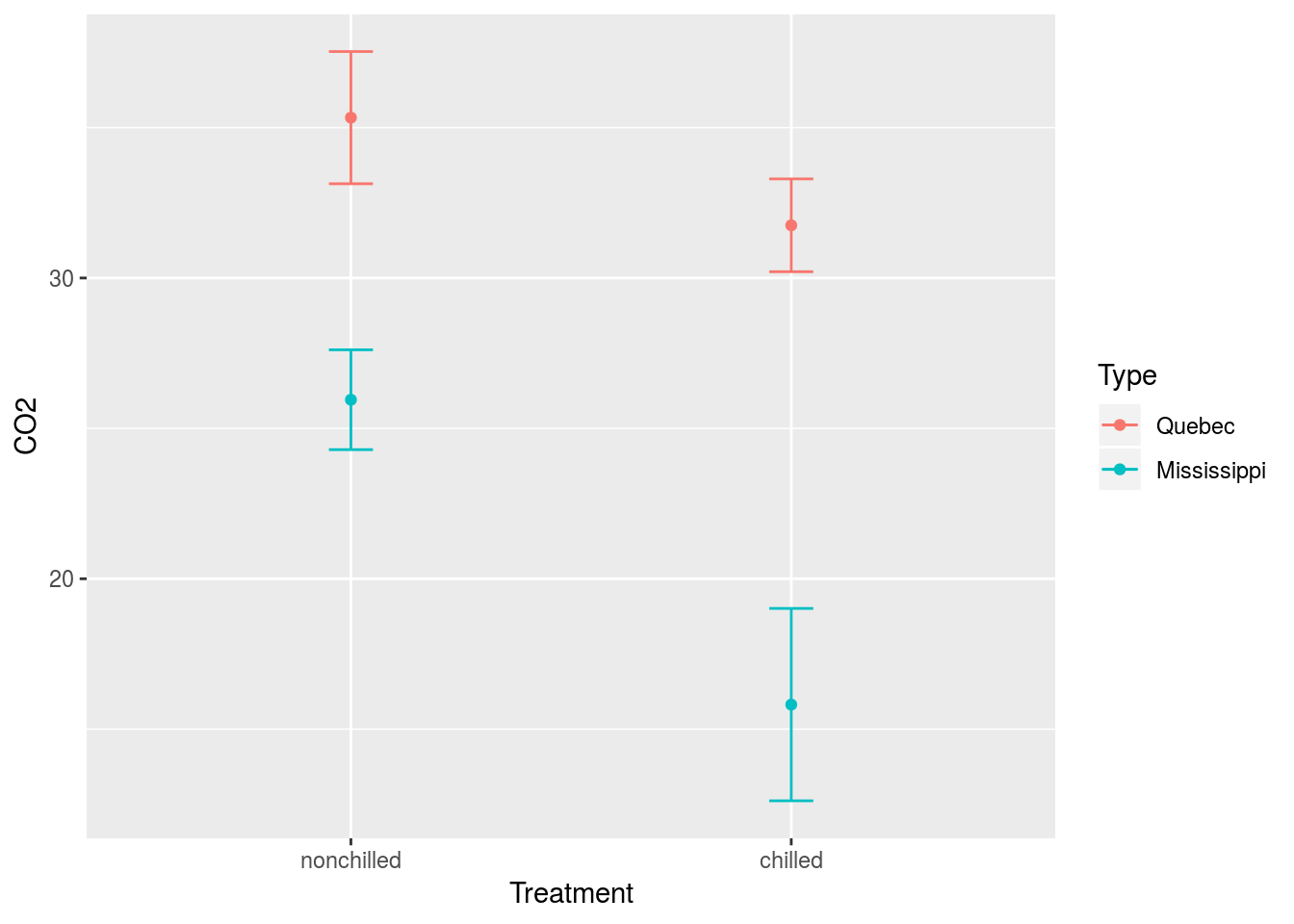
5.3 Tarea 1
La municipalidad de Muy muy lejano tiene un sistema de 5 lagos muy contaminados. Se le encarga estudiar la capacidad biorremediadora de las algas unicelulares Chlorellia fecolitica (desde ahora alga A) y Rhodollia coprofaga (en adelante alga B). Para realizar el experimento y posteriormente comprar cepas para biorremediación. Con un presupuesto de 50,000 coronas, donde cada cultivo de alga cuesta 1,000 coronas. Utilizando la siguiente app realize un experimento, y luego genere un informe en formato paper donde aparezca lo siguiente:
- Realiza un calculo de poder en base al archivo Presamp.csv para ver cual debiera ser tu número de mustras necesaria y explicalo
- Establece si se cumplen los supuestos de los test a realizar y ejecuta deacurdo a tus conocimientos justificando
- Determinar si alguna de las algas es mejor biorremediador (incluyendo comparaciones post-hoc)
- Dentro de lo posible utiliza la menor cantidad posible de presupuesto, debes utilizar el presupuesto que te queda para proponer una medida de biorremediación
5.4 Referencias
Referencias
Tukey, John W. 1977. “Some Thoughts on Clinical Trials, Especially Problems of Multiplicity.” Science 198 (4318). American Asociation for the Advancement of Science: 679–84.
Morgan, John F. 2007. “P Value Fetishism and Use of the Bonferroni Adjustment.” Evidence-Based Mental Health 10 (2). BMJ Publishing Group LTD: 34.