Capítulo 1 Tipos de modelos: Predictivos vs Explicativos

En este capítulo se explicará que es un modelo estadísitco, y como evaluar su capacidad explicativa y/o preditiva. Además, hablaremos de los criterios de información y como estos nos ayudan a tener un balance entre predicción y explicación.

1.1 Paquetes necesarios para este capítulo

Para este capitulo necesitas tener instalado los paquetes tidyverse (Wickham 2019), broom (Robinson and Hayes 2020), MuMIn (Bartoń 2019) y caret (Kuhn 2020)

1.1.1 Presentación html

Puedes seguir la clase de los videos en el siguiente link

y ver la clase nuevamente en el sigueinte video

1.2 Modelos explicativos y predictivos

1.2.1 Modelos estadísticos

Un modelo estadístico es un modelo no determinista que utiliza una muestra de una población para intentar determinar patrones de esta población. En ese sentido un ANOVA (Análisis de varianza), una regresión lineal, una regresión no lineal son modelos estadísticos.

En un modelo estadístico muchas veces podemos medir su poder explicativo y su poder predictivo, en este curso aprenderemos varios parametros para medir estas carácteristicas en varios modelos. Una de las medidas más conocidas para tratar de medir el poder predictivo de un modelo es el \(R^2\) de una regresión lineal, donde usualmente si tenemos por ejemplo un \(R^2\) de 0.74, es usual el decir que el modelo explica el 74% de variación de la variable respuesta. Siguiendo ese ejemplo, una forma fácil de medir el poder predictivo de un modelo (pero no el mejor), es medir el \(R^2\) de las predicciones del modelo en una nueva base de datos.

1.2.1.1 Ejemplo

¿Podemos explicar o predecir la eficiencia de combustible (mpg) a partir de los caballos de fuerza (hp) de un Vehículo? Veamos el patrón que se observa en la Figura 1.1

ggplot(mtcars, aes(x = hp, y = mpg)) + geom_point() + theme_classic()

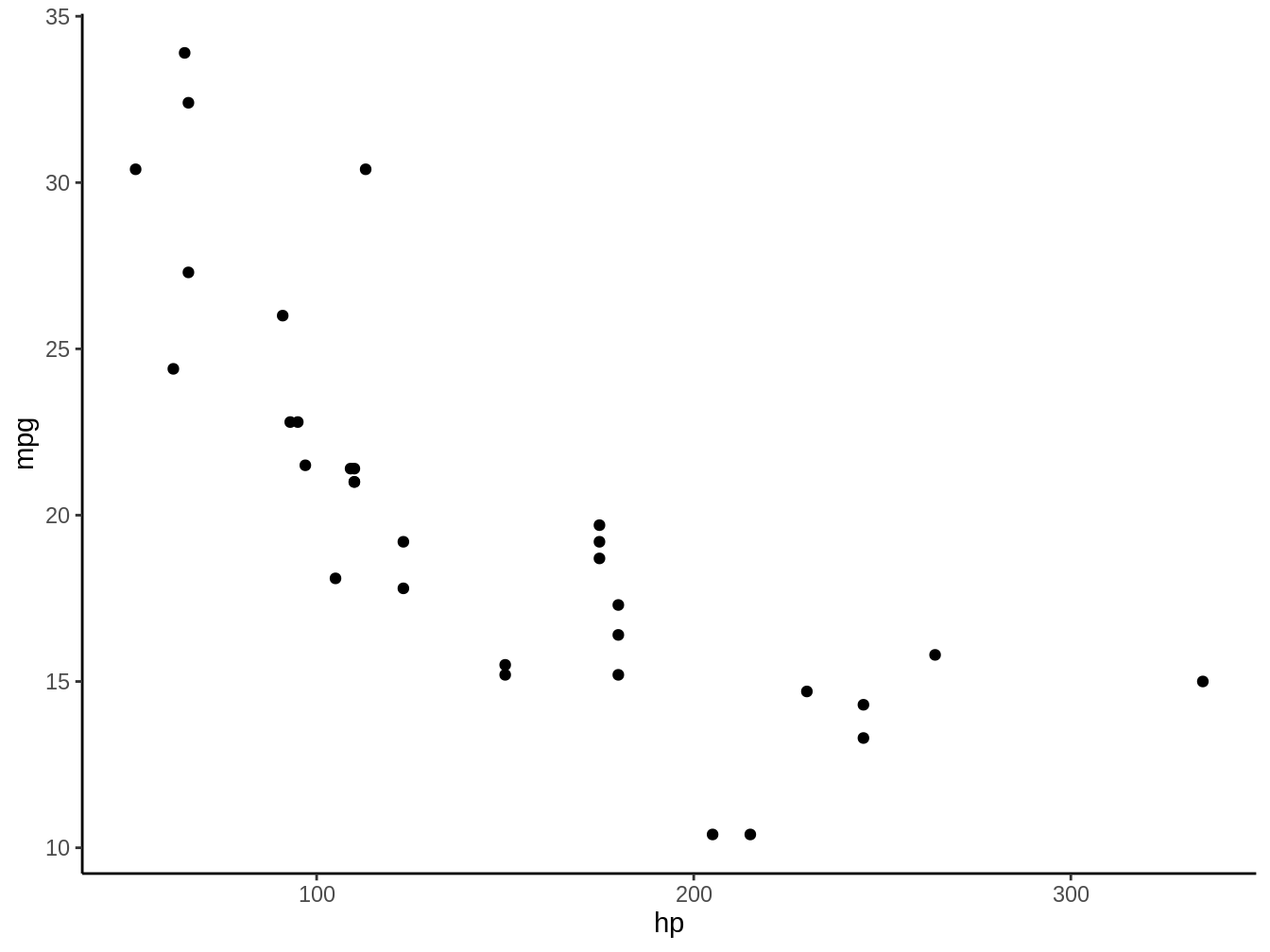
Figura 1.1: Caballos de Fuerza de un vehículo (HP) graficados contra la eficiencia en millas por galon (mpg) del mismo vehículo

Claramente vemos que en general a medida que aumentan los caballos de fuerza disminuye la eficiencia de los vehículos, lo cual sería nuestra hipótesis

1.2.1.2 Primer paso separar en base de datos de entrenamiento y de testeo

En este caso queremos probar el poder explicativo y predictivo de esta base de datos, por lo cuál dividiremos nuestra base de datos en dos una base de datos de entrenamiento, con la cual ajustaremos el modelo y una de testeo o de prueba, en la cual veremos el poder predictivo del modelo con una base de datos que el modelo no ha visto anteriormente.

Para esto utilizamos el siguiente código

set.seed(2018)
index <- sample(1:nrow(mtcars), size = round(nrow(mtcars)/2))

Train <- mtcars[index,]

Test <- mtcars[-index,]

Esto genera la base de datos Train que tiene 16 observaciones y la base de datos Test que tiene 16 observaciones independientes. En este caso nuevamente si vemos la figura 1.1, vemos que la relación entre los caballos de fuerza y la eficiencia no parecen ser particualrmente lineales, por lo que testearemos el siguiente modelo estadístico:

\[mpg = \beta_1 hp + \beta_2 hp^2 + c\]

Para determinar el poder tanto explicativo como predictivo del modelo, lo primero que haremos será crear el objeto Modelo usando un modelo lineal simple lm

Modelo <- lm(mpg ~ hp + I(hp^2), data = Train)

1.2.1.3 Poder explicativo:

Primero veamos el poder predictivo de este modelo, para eso usaremos la función glance del paquete broom

glance(Modelo)

kable(glance(Modelo) %>% dplyr::select(r.squared, p.value, df), caption = "R cuadrado, valor de p y grados de libertad del modelo")  %>% kable_styling(bootstrap_options = c("striped", "hover"))

Tabla 1.1: R cuadrado, valor de p y grados de libertad del modelo
r.squared	p.value	df
0.7879861	4.18e-05	3

Como vemos en la Tabla 1.1, nuestro modelo tiene un poder explicativo bastante bueno, donde con solo saber los caballos de fuerza de un vehículo, podemos explicar un 78.8% de la variación en la eficiencia del vehículo.

Usando la función predict, podemos ver la predicción del modelo con nuestra base de datos original, ademas si vemos la tabla 1.2, vemos la predicción el observado y los residuales, que es la resta entre lo observado y la predicción. Además en la 1.2 podemos ver en la linea segmentada la predicción del modelo comparado con los datos en los puntos

Train$Pred <- predict(Modelo, Train)

kable(Train %>% dplyr::select(hp, mpg,  Pred) %>% mutate(resid = Pred - mpg), caption = "En esta tabla podemos observar para cada observación los caballos de fuerza, la predicción y los residuales para cada observación")  %>% kable_styling(bootstrap_options = c("striped", "hover"))

Tabla 1.2: En esta tabla podemos observar para cada observación los caballos de fuerza, la predicción y los residuales para cada observación
hp	mpg	Pred	resid
205	10.4	14.14298	3.7429788
150	15.2	16.82526	1.6252606
93	22.8	23.11205	0.3120512
180	16.4	14.95019	-1.4498054
180	17.3	14.95019	-2.3498054
66	32.4	27.33590	-5.0640977
97	21.5	22.55441	1.0544133
95	22.8	22.83103	0.0310349
123	17.8	19.35825	1.5582506
62	24.4	28.02978	3.6297759
264	15.8	14.96047	-0.8395335
109	21.4	20.98697	-0.4130274
150	15.5	16.82526	1.3252606
245	13.3	14.27971	0.9797112
110	21.0	20.86349	-0.1365061
175	19.2	15.19404	-4.0059616

ggplot(Train, aes(x = hp, y = mpg)) + geom_point() + geom_line(aes(y = Pred), color = "red", lty = 2) + theme_classic()

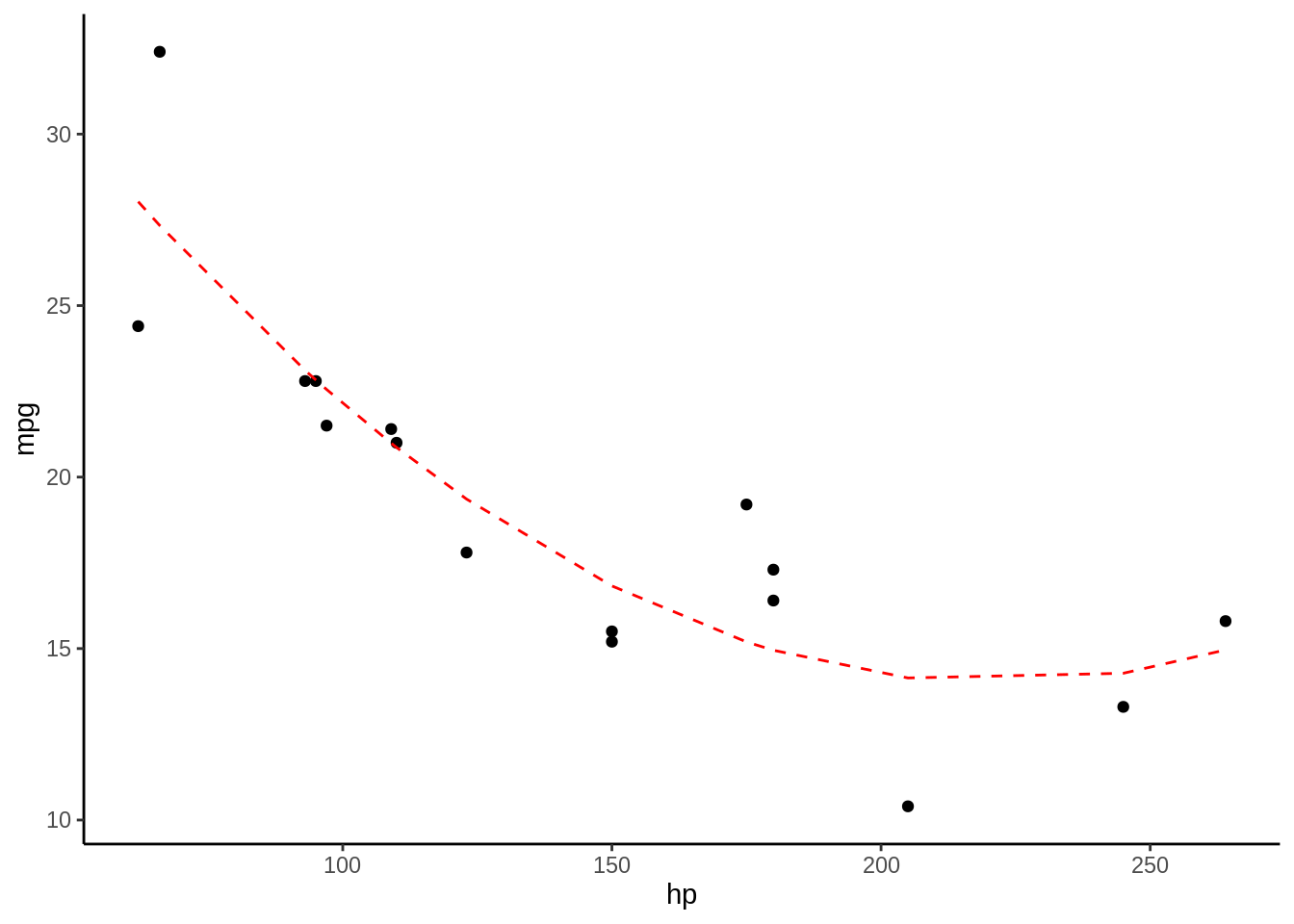
Los puntos representan las observaciones con las que se entrenó el modelo, la linea roja segmentada representa la predicción del modelo

Figura 1.2: Los puntos representan las observaciones con las que se entrenó el modelo, la linea roja segmentada representa la predicción del modelo

1.2.1.4 Poder Predictivo:

Para determinar el poder predictivo de un modelo, tenemos que probar su predicciones con una base de datos que no haya sido usada para ajustar el modelo, es para eso que generamos la base de datos Test, lo primero que debemos hacer para ver el poder predictivo del modelo es usar el modelo con esta base de datos nueva, y generear predicciones, para esto nuevamente usamos la función predict

Test$Pred <- predict(Modelo, Test)

Posteriormente, usamos la funcion postResampledel paquete caret, usando dos argumentos. En el argumento pred usamos los valores predichos con el modelo, y en el argumento obs usamos los valores observados, es decir, los que esperamos que nos entregue el modelo:

library(caret)
postResample(pred = Test$Pred, obs = Test$mpg)

##      RMSE  Rsquared       MAE 
## 3.8741375 0.6805523 2.6437118

La tabla resultante de esta función nos entrega varios valores para determinar que tan buena es la predicción (Mean Square Error, R Cuadrado y Mean Absolute Error), estos valores los estudiaremos mas adelante en los capítulos de Machine Learning, pero por ahora quedemonos con el valor de R Cuadrado, que es igual a 0.68, un valor menor al 0.79 del poder predictivo, lo cual es de esperarse. Casi siempre el valor predictivo de un modelo es menor al valor explicativo de este mismo. En la tabla 1.3 y en la figura 1.3 podemos ver las predicciones del modelo.

kable(Test %>% dplyr::select(hp, mpg,  Pred) %>% mutate(resid = Pred - mpg), caption = "En esta tabla podemos observar para cada observación los caballos de fuerza, la predicción y los residuales para cada observación")  %>% kable_styling(bootstrap_options = c("striped", "hover"))

Tabla 1.3: En esta tabla podemos observar para cada observación los caballos de fuerza, la predicción y los residuales para cada observación
hp	mpg	Pred	resid
110	21.0	20.86349	-0.1365061
110	21.4	20.86349	-0.5365061
175	18.7	15.19404	-3.5059616
105	18.1	21.49187	3.3918740
245	14.3	14.27971	-0.0202888
123	19.2	19.35825	0.1582506
180	15.2	14.95019	-0.2498054
215	10.4	14.01236	3.6123606
230	14.7	14.02243	-0.6775651
52	30.4	29.84137	-0.5586329
65	33.9	27.50772	-6.3922773
66	27.3	27.33590	0.0359023
91	26.0	23.39746	-2.6025378
113	30.4	20.49965	-9.9003501
175	19.7	15.19404	-4.5059616
335	15.0	21.01461	6.0146090

ggplot(Test, aes(x = hp, y = mpg)) + geom_point() + geom_line(aes(y = Pred), color = "red", lty = 2) + theme_classic()

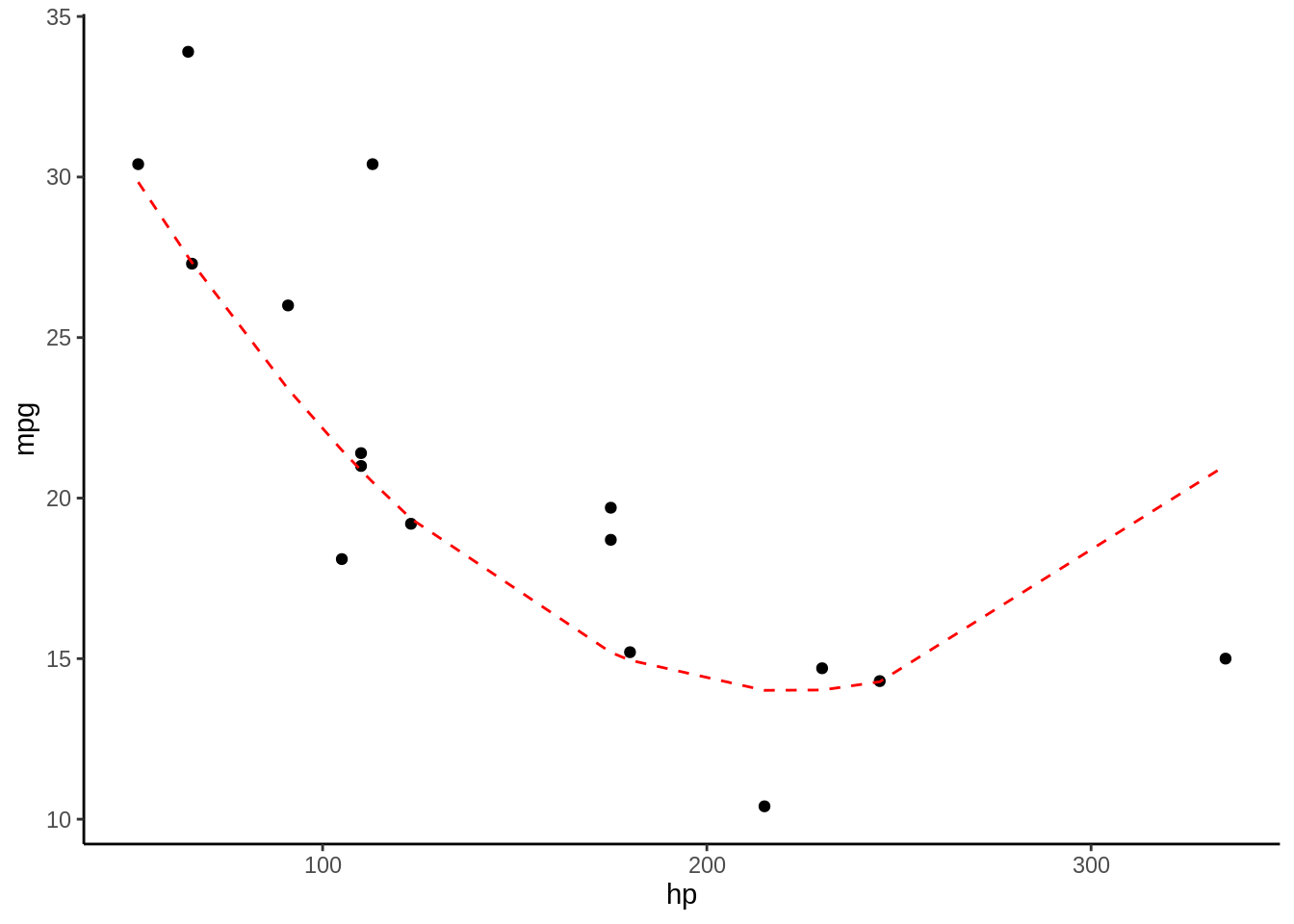
Figura 1.3: Los puntos representan las observaciones con las que se entrenó el modelo, la linea roja segmentada representa la predicción del modelo

1.3 Sobreajuste

1.3.1 Que pasa al complejizar el modelo

El modelo que evaluamos tenia un terminlo lineal \(\beta_1 hp\) y uno cuadrático \(\beta_2 hp^2\), pero el poder tanto explicativo como predictivo podría mejorar o empeorar si agregamos un termino cúbico \(\beta_3 hp^3\) o uno elevado a la cuarta \(\beta_4 hp^4\), ¿Que ocurre con el poder explicativo y/o el predictivo cuando aumentamos la complejidad del modelo?

Para este ejemplo, veremos que ocurre con el \(R^2\) explicativo a medida que aumentamos la complejidad del modelo desde \(K = 1\), esto es solo un intercepto, pasando por el modelo lineal \(K = 2\), modelo cuadratico \(K = 3\) hasta llegar a agregar el argumento elevado a 12:

\[mpg = \beta_1 hp + \beta_2 hp^2 + ... + \beta_12 hp^{12} c\]

Al observar como se comporta el poder explicativo, vemos que aumenta siempre que agregamos parametros como vemos en la animación de la figura 1.4, en esta vemos que el \(R^2\) siempre aumenta, y que la linea roja que marca la predicción del modelo, sigue de forma casi perfecta los puntos de la base de datos Train, si esto es así, por que no usamos siempre el modelo más complejo, lo veremos en la siguiente sección donde hablaremos del Sobreajuste.

knitr::include_graphics("Explicativo.gif")

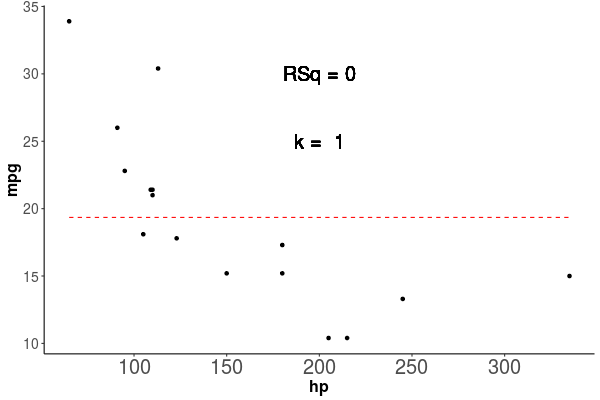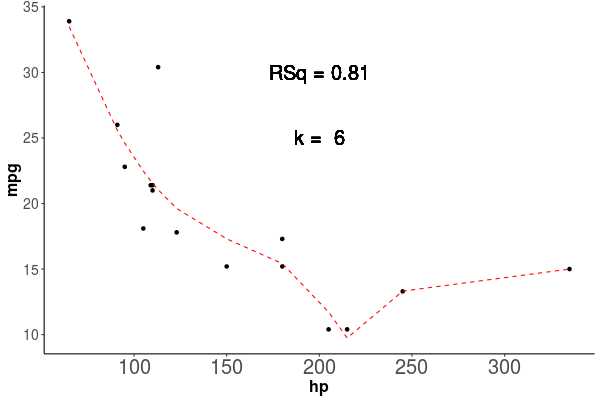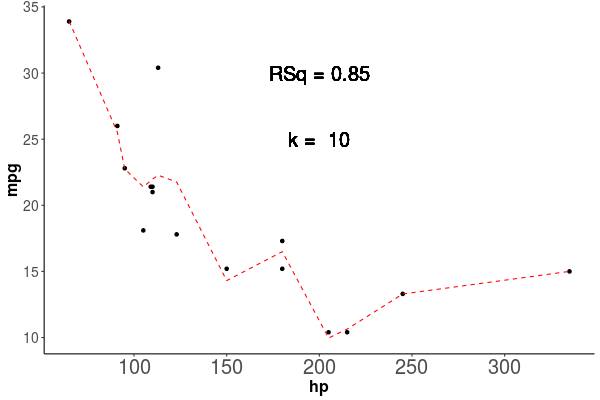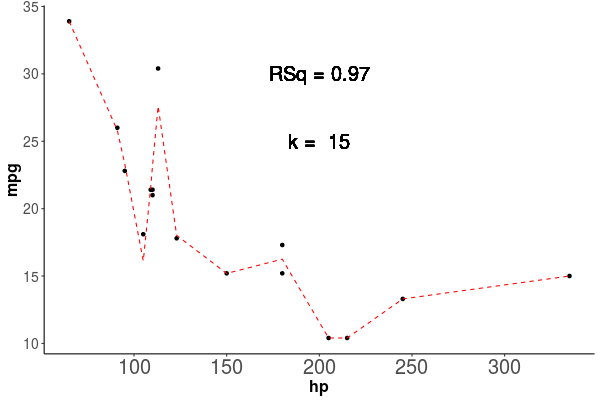
Figura 1.4: Los puntos representan las observaciones con las que se entrenó el modelo, la linea roja segmentada representa la predicción del modelo

1.3.2 Sobreajuste

El sobreajute ocurre cuando por aumentar el ajuste de un modelo (\(R^2\) por ejemplo), generamos un modelo tan complejo, que practicamente no tiene error con la base de datos que lo entrenamos, sin embargo, al probarlo con una nueva base de datos, vemos que el modelo es muy malo para predecir sobre una nueva base de datos, esto es el modelo se ha vuelto idiosincrático, y creemos que es un buen modelo, pero solo para los datos que usamos para el modelo mismo. Esto podemos verlo en la figura 1.5, en esta vemos como en el gráfico de la izquierda, a medida que aumentamos el número de parametros, siempre aumenta nuestro \(R^2\), en el gráfico de la derecha sin embargo, vemos que desde los 6 parametros en adelante, el modelo es peor en su predicción que sobre la base de datos original, y ya cuando tenemos 8 parametros, la diferencia es muy alta, con un \(R^2\) de 0.83 para la base de datos original, y 0.3 para la base de datos de prueba, en ese momento, el modelo ya esta sobreajustado.

knitr::include_graphics("Predictivo.gif")

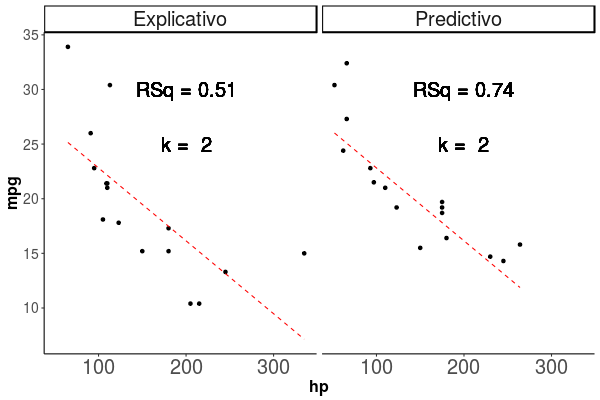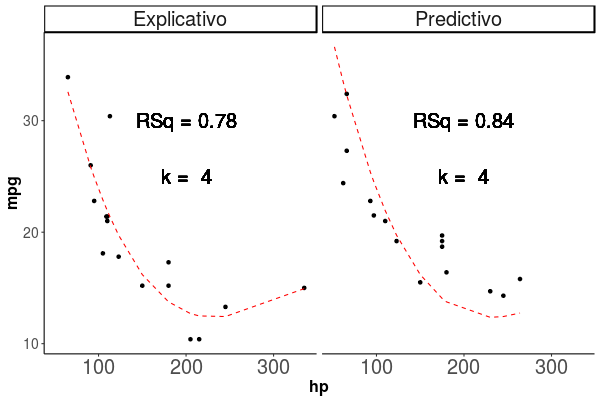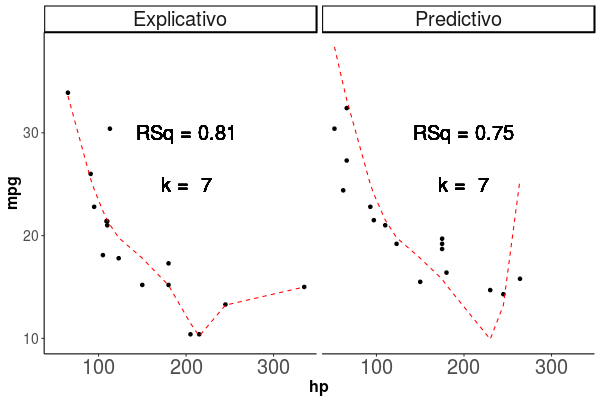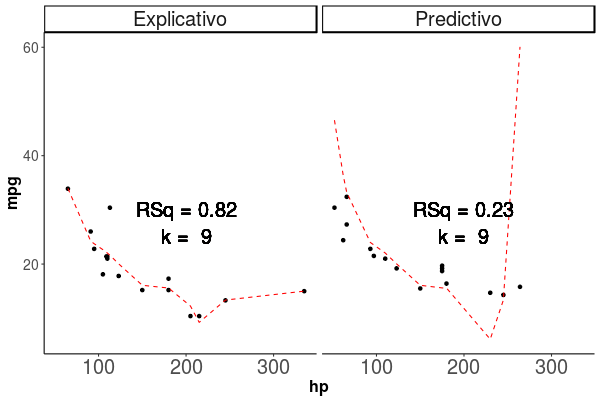
El gráfico de la Izquerda muestra el ajuste del modelo en los datos en que se entrenó el modelo, mientras que el de la derecha, sobre la base de datos de prueba. Los puntos representan las observaciones con las que se entrenó el modelo, la linea roja segmentada representa la predicción del modelo

Figura 1.5: El gráfico de la Izquerda muestra el ajuste del modelo en los datos en que se entrenó el modelo, mientras que el de la derecha, sobre la base de datos de prueba. Los puntos representan las observaciones con las que se entrenó el modelo, la linea roja segmentada representa la predicción del modelo

1.3.3 ¿Cuando me puede interesar el maximizar el poder predictivo?

Hay momentos en los cuales me preocupa el poder predictivo y no me interesa la explicación, algunos ejemplos de esto son:

Texto predictivo del celular
Auto-corrector
Efectos de cambio climático
Detección de caras en redes sociales

Para seleccionar el modelo con mayor poder predictivo, se debe maximizar el desempeño de la metrica en la base de datos de prueba (Test), en el caso que explicamos anteriormente ese valor es \(R^2\). Esto es muy importante tenerlo en mente, es el principio básico de cuando empezemos a trabajar con Machine Learning en capítulos posteriores.

1.3.4 ¿Cuando me puede interesar el maximizar el poder explicativo?

En otros casos lo que mas me interesa es el poder explicar un fenómeno, sin importar que pueda hacer predicciones en una base de datos nueva, por ejemplo:

Pruebas a hipótesis causales
¿Que causa el cambio climático?

En general para trabajar bajo esta aproximación debemos seguir los siguientes pasos:

Generación de hipótesis (plural)
Generación de modelos para cada hipótesis
Interpretación de resultados en base a modelos e hipótesis

1.4 Explicación o Predicción?

knitr::include_graphics("Dilema.jpg", dpi = 80)

Figura 1.6: Que hacer?

via GIPHY

En la mayoría de los casos, lo que más nos interesa es el tratar de encontrar un balance entre el poder predictivo y el explicativo, no queremos tomar la decición de la la figura 1.6. Por un lado el maximizar el poder explivativo, lleva a modelos muy particulares, que solo explican la base de datos que usamos para entrenar el modelo, lo cual puede no aplicar a una nueva base de datos, (por ejemplo podemos hacer un gran modelo que explique en un 99% la variación en el exito reproductivo de huemules en los altos de Chillán, pero esto puede no explicar ni un 10% de la variación del exito reproductivo de la misma especie en el Parque Nacional Bernardo O’Higgins) ¿Como hacer para balancear el poder explicativo y predictivo? Usando criterios de Información.

1.4.1 Criterio de Información de Akaike

El Criterio de Información de Akaike (Akaike 1974) (AIC de aquí en adelante por sus siglas en inglés Akaike Information Criterion), es un criterio basado en teoría de información, el cual balancea bastante bien el poder explicativo y predictivo, para esto castiga el uso de muchas variables o parametros en un modelo (\(K\)), algo difícil de entender del AIC cuando empezamos a trabajar con el, es que no existen valores buenos o malos de AIC, sinó que todo tiene que ver con la comparación entre modelos que compiten entre sí, y en general a menor AIC, mejor es el modelo, la siguiente es la formula de AIC:

\[AIC = 2k - \ln(L)\]

Existe además una formula de AIC corregido (AICc) (Cavanaugh 1997), el cual incorpora el número de observaciones en el calculo del criterio, como vemos en la siguiente formula, n se encuentra en el denominador de el segundo término que se suma a AIC:

\[AICc = AIC + \frac{2k^2 + 2k}{n-k-1}\]

Esto implica que cuando n tiende a infinito, AICc es casi igual a AIC, por lo cual siempre se recomienda el uso de AICc sobre AIC. Usualmente una diferencia de 2 en AIC, se considera “Significativa” (Anderson and Burnham 2004)

Para calcular AICc podemos usar la función AICc en MuMIn, en el siguiente código, generamos un modelo en el cual usando la base de datos mtcars, en el cual ajustamos un modelo lineal, donde vemos si la eficiencia de un vehículo puede ser explicada por los caballos de fuerza en su forma lineal y cuadrática:

library(MuMIn)
Modelo <- lm(mpg ~ hp + I(hp^2), data = Train)
AICc(Modelo)

## [1] 84.02319

AICc no es el único criterio de información, en el paquete MuMIn, existen otros como BIC, CAIFC, DIC y QAIC. En ecología y lo más habitual es usar AICc, en algunos campos experimentales es habitual BIC, para más sobre esto ver (Aho, Derryberry, and Peterson 2014). En otros casos por sobredispersión existen otros Criteros de información (Kim et al. 2014)

1.4.2 Relación entre AICc y R cuadrado

Como fue prometido en la sección 1.4, el AICc intenta balancear explicación con predicción, y para ello, busca que aumente la métrica explicativa (en este caso \(R^2\)), pero para agregar un parámetro extra el \(R^2\) tiene que aumentar bastante. En la Figura 1.7, vemos las medidas de AICc y \(R^2\) para los mismos modelos.

library(MuMIn)
library(tidyverse)

Fit1 <- glm(mpg ~., data = mtcars)
options(na.action = "na.fail")
dd <- dredge(Fit1, extra = "R^2")
dd <- as.data.frame(dd) 
colnames(dd) <- make.names(colnames(dd))
SUMM <- dd %>% group_by(df) %>% summarize(RSq = max(R.2), AICc = min(AICc))

dfAICmin <- filter(SUMM, AICc == min(AICc))$df

SUMM <- SUMM %>% pivot_longer(-df)

ggplot(SUMM, aes(x = df, y = value)) + geom_line() + geom_point() + facet_wrap(~name, scales = "free_y", strip.position = "left") + theme_bw() + ylab("") + geom_vline(xintercept =dfAICmin, col = "red") + xlab("Número de parámetros") + scale_x_continuous(breaks = c(3, 5, 7, 9, 11))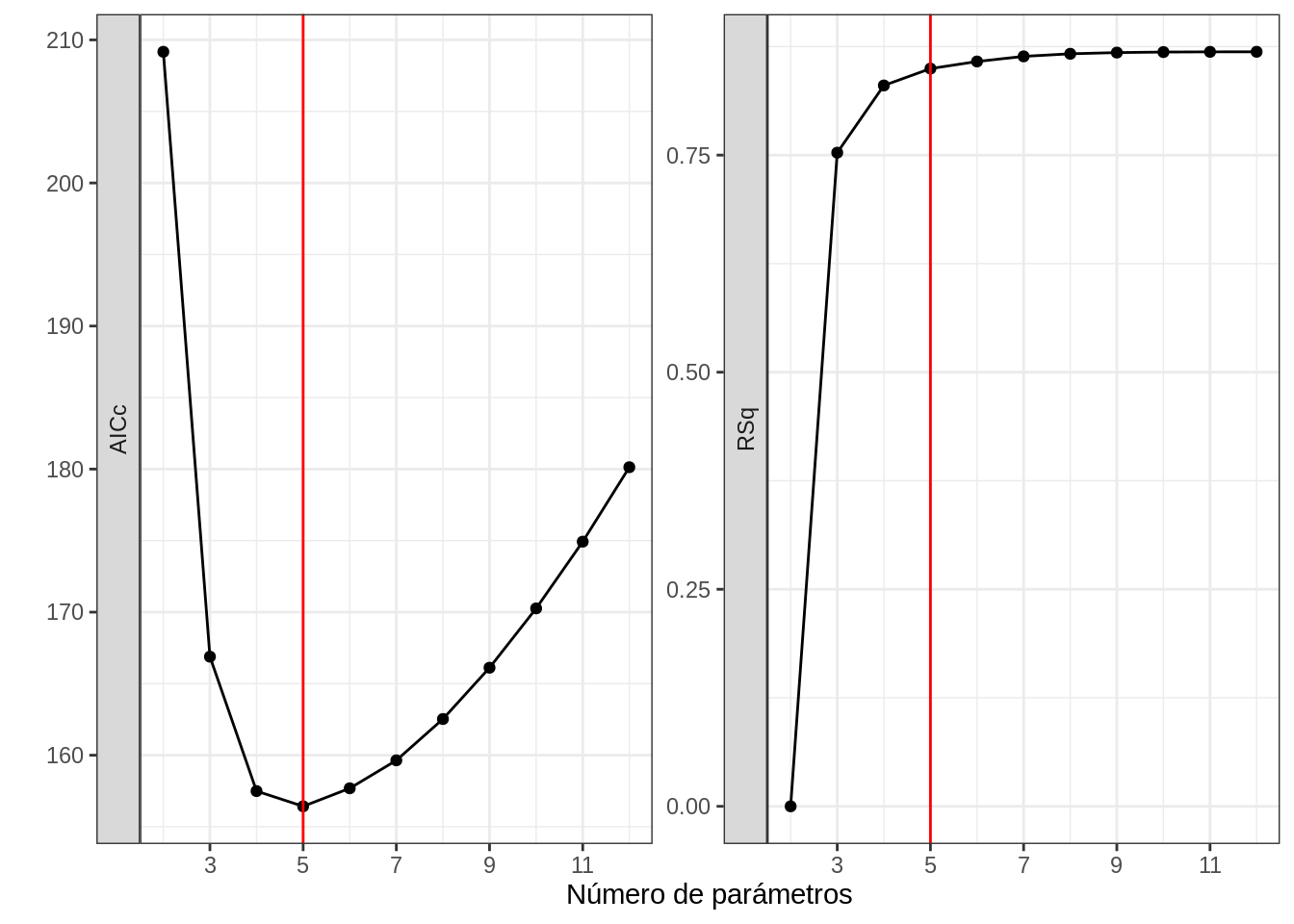

Figura 1.7: Relación entre AICc y R cuadrado

La linea roja corresponde al modelo con AICc más bajo, el cual corresponde a un modelo con 5 parámetros (ver figura 1.7, panel izquierdo), en el panel derecho, vemos que en ese momento el aumento de \(R^2\) disminuye en pendiente. El mejor modelo de 5 parametros tiene un \(R^2\) de 0.850 y el mejor modelo de 6 parámetros tiene un \(R^2\) de 0.858. Lo que nos esta diciendo el AICc en resumen es ¿Vale la pena agregar un parametro más y arriesgar un sobreajuste por aumentar el \(R^2\) en 0.08? Probablemente no.

1.5 Ejercicio

Tomando la base de datos mtcars explora la relacion entre AICc, \(R^2\) Exploratorio y \(R^2\) Predictivo.

Para eso genera un data frame con las siguientes columnas:

AICc
K
\(R^2\) Exploratorio
\(R^2\) Predictivo
Id modelo
Hasta 11:30

1.6 Mensaje final

	Predicción	Explicación
Relación x e y	Asociación	Causalidad
Relación función modelos	Datos	Teoria
Visión	Futura	Retrospectiva
Varianza	Maximizar predicción	Minimizar sesgo

References

Aho, Ken, DeWayne Derryberry, and Teri Peterson. 2014. “Model Selection for Ecologists: The Worldviews of Aic and Bic.” Ecology 95 (3). Wiley Online Library: 631–36.

Akaike, Hirotugu. 1974. “A New Look at the Statistical Model Identification.” In Selected Papers of Hirotugu Akaike, 215–22. Springer.

Anderson, D, and K Burnham. 2004. “Model Selection and Multi-Model Inference.” Second. NY: Springer-Verlag 63.

Bartoń, Kamil. 2019. MuMIn: Multi-Model Inference. https://CRAN.R-project.org/package=MuMIn.

Cavanaugh, Joseph E. 1997. “Unifying the Derivations for the Akaike and Corrected Akaike Information Criteria.” Statistics & Probability Letters 33 (2). Elsevier: 201–8.

Kim, Hyun-Joo, Joseph E Cavanaugh, Tad A Dallas, and Stephanie A Foré. 2014. “Model Selection Criteria for Overdispersed Data and Their Application to the Characterization of a Host-Parasite Relationship.” Environmental and Ecological Statistics 21 (2). Springer: 329–50.

Kuhn, Max. 2020. Caret: Classification and Regression Training. https://CRAN.R-project.org/package=caret.

Robinson, David, and Alex Hayes. 2020. Broom: Convert Statistical Analysis Objects into Tidy Tibbles. https://CRAN.R-project.org/package=broom.

Wickham, Hadley. 2019. Tidyverse: Easily Install and Load the ’Tidyverse’. https://CRAN.R-project.org/package=tidyverse.