Capítulo 2 Selección de modelos
2.1 Paquetes necesarios para este capítulo
Para este capitulo necesitas tener instalado los paquetes tidyverse (Wickham 2019), broom (Robinson and Hayes 2020) y MuMIn (Bartoń 2019)
2.1.1 Presentación html
Puedes seguir la clase de los videos en el siguiente link
y ver la clase en vivo desde las 20:30 horas el día martes 5 de Mayo del 2020 a continuación
2.2 Alcance de la inferencia multimodelo
La inferencia Multimodelo (Anderson and Burnham 2004) es un campo teórico de la estadística que nos perminte tomar decisiones equilibrando el poder predictivo y explicativo de multiples modelos en competencia, y nos da un marco de acción para seleccionar entre distintos modelos, dentro de esto, seleccionar el o los modelos más parsimoniosos entre varios en competencia, no el que predice más
2.2.0.1 Que es lo que no nos permite la inferencia multimodelo
Si bien la Inferencia Multimodelo es una herramienta muy poderosa, hay varios problemas previos que no puede arreglar, entre ellos está un estudio mal diseñado y una pobre selección de variables a explicar un problema. Por otro lado, es importante recordar que la Inferencia Multimodelo no es una receta, hay mucho de criterio y desiciones que tomar en base a nuestro conocimiento del sistema a modelar.
2.2.1 Que necesitamos para realizar inferencia multimodelo
Antes de intentar seleccionar entre modelos, hay varios pasos a seguir, lo primero es generar un buen diseño de muestreo o diseño experimental para nuestra base de datos y pregunta, luego debemos generar las hipótesis de forma muy cuidadosa y detallada, y finalmente (y quizás lo más importante para este curso), la selección adecuada de variables para distinguir entre hipótesis.
2.3 Generación de hipótesis
Partamos con una base de datos, utilizaremos la base de datos de kaggle de expectativa de vida que encontramos en el el siguiente link (Rajarshi 2018), y que he modificado, aquí esta el código para bajar la versión simplificada y modificada por mi:
URL <- download.file("https://github.com/derek-corcoran-barrios/derek-corcoran-barrios.github.io/raw/master/CursoMulti/LifeExpect.rds", "LifeExpect.rds")
Life_Expect <- readRDS("LifeExpect.rds")Las variables que podemos utilizar para crear hipotesis son Country, Life.expectancy, Alcohol, percentage.expenditure, Total.expenditure, GDP, Population, thinness..1.19.years, Schooling, Year, podemos ver una esplicación de cada una de estas variables en su descripción en kaggle.
2.3.1 Hipótesis 1: nula negativa
Para partir, estableceremos un modelo nulo negativo, donde la expectativa de vida no es explicada por nada, es decir, no cambia de acuerdo a nunguna de nuestras variables:
2.3.2 Hipótesis 2: nula positiva
Luego partiremos con un modelo en el cual solo el país y el paso del tiempo explican el cambio en la espectativa de vida, so vemos en la Figura 2.1, cada país parece tener una historia bastante consistente, donde por lo general en cada uno, la espectativa de vida parece aumentar en el tiempo.
Figura 2.1: Expectativa de vida por año y país, cada linea de color representa un país distinto
Esto lo usaremos como un modelo nulo positivo, esto es, la espectativa cambia con el paso del tiempo en cada país independiente de las desiciones y políticas públicas que tomen. Esto es, no importa cuanto del Producto Interno Bruto se invierta en salud, ni cuanta educación haya en el país, esto no afectará en la expectativa de vida:
Todas las hipóteses siguientes tomarán este modelo de base y agregaremos variables para hipótesis específicas
2.3.3 Hipótesis 3: económica
En este caso tomaremos solo las variables económicas, esto es percentage.expenditure que es el gasto en salud, como porcentaje de PIB per cápita; Total.expenditure Gasto general del gobierno en salud como porcentaje del gasto total del gobierno y GDP que es el producto Interno Bruto por persona en dolares.
Lo que estamos suponiendo en este modelo es que la administración económica del gobierno es lo que mejor explica la expectativa de vida
2.3.4 Hipótesis 4: educativa
En esta hipótesis asumimos que la educación del país es lo que nos lleva a tener una mayor expectativa de vida. Para esto usamos la variable Schooling que es el número de años de escolaridad promedio en el país.
2.3.5 Hipótesis 5: educativa y económica
En esta hipótesis decimos que no es la educación ni la economía por si solas las que explican la expectativa, sinó que ambas en conjunto
Para continuar debemos hacer una lista con todos los modelos e hipotesis a testear
2.4 Selección de modelos
La selección de modelos la realizaremos en base a su valor de AICc utilizando la función model.sel del paquete MuMIn, para esto solo debemos dentro de la función poner como argumento la lista de modelos que creamos en la sección anterior.
Como comentamos en el Capítulo 1, a menor valor de AICc, mejor el modelo, como vemos en la tabla anterior. Como vemos según esto, el mejor modelo de acuerdo a nuestras hipótesis es el modelo educativo, seguido del educativo mas económica, un poco mas abajo encontramos la hipotesis nula positiva, es decir, solo país y año, el cuarto modelo es el modelo economico y finalmente con mucha diferencia el modelo nulo educativo, en este momento puedo seleccionar modelos bajo varios criterios
2.4.1 Delta AICc
Este es el método mas habitual, lo más típico es quedarse con los modelos que tienen un \(\Delta AICc\) de máximo dos (Anderson and Burnham 2004), en este caso solo hay uno con esas carácteristicas, que es el modelo educativo, el segundo (el más complejo) tiene un \(\Delta AICc\) de 2.789, y por eso siguiendo esta metodología nos quedamos con el primero, el mejor modelo. Para hacer esto programáticamente usando MuMIn, seguimos los siguientes pasos:
Primero generamos la tabla con \(\Delta AICc\) de 2:
Lo cual nos dá la siguiente tabla:
Si comparamos esta tabla con la anterior, veran que la columna de los pesos de akaike cambian para los mimos modelos entre una y otra tabla, esto será explicado en detalle en la seccion 2.4.2.
Luego con el siguiente código seleccionamos el mejor modelo y podemos ver sus carácteristicas y parametros usando las funciones glance y tidy de broom:
Como en la tabla anterior, el modelo tiene un \(R^2\) de 0.96 y el mismo \(R^2\) ajustado, esto es, sin necesidad de agregar ningún factor económico podemos explicar un 96% de la variación, en la tabla siguiente podemos ver los parámetros del modelo, el cual nos dice que por cada año extra de educación, hay un aumento de 0.139 años en la espectativa de vida, y que además cada año que pasa, la espectativa de vida aumenta en 0.362 años.
2.4.2 Pesos de Akaike
Otra forma de seleccionar modelos de forma más conservadora es usando los pesos de Akaike, estos pesos usan el log likelihood para comparar probabilidad proporcional de cada modelo de ajustarse a los datos, en este caso, por ejemplo, ek mejor modelo (educacion), tiene un peso de akaike de 0.74, mientras que el segundo mejor modelo (educación y economía) tiene un peso de 0.18, para ver que tanto más plausible es el modelo educativo que el educativo y economico simplemente dividimos los pesos y esto nos dice que el modelo educativo es 4.03 veces mas probable que el educativo y económico a ajustarse a los datos.
Usualmente al seleccionar por pesos de akaike, tomamos todos los modelos y seleccionamos los que tienen un peso sumado de akaike de al menos 0.95, para eso usamos el siguiente código, el cuál selecciona dos de los seis modelos, el Educativo y el Educativo más Económico. Cuando seleccionamos por método de \(\Delta AICc\) teníamos un solo modelo, por lo que no teníamos problema ¿que hacemos en este caso?, lo veremos en la sección 2.5
2.5 Promediar modelos
2.5.1 Promediar modelos usando MuMIn
En la sección 2.4.1, usando \(\Delta AICc\) seleccionamos un solo modelo, y nos quedamos con ese, pero en la sección 2.4.2 usando Pesos de Akaike tenemos dos modelos seleccionados. Cuando tenemos más de un modelo seleccionado según la metodología elegida debemos promediar modelos. Para esto hay dos metodologías distintas, el metodo completo (full) y el metodo subset, usaremos la variable percentage.expenditure para mostrar como funciona cada uno de esos métodos y como se calcula el parámetro final.
Lo primero que haremos para ejemplificar este problema es el generar un data frame con solo el estimador de esa variable y el peso de akaike de la misma (ver tabla 2.1)
| percentage.expenditure | weight | |
|---|---|---|
| 4 | NA | 0.8013277 |
| 5 | 6.06e-05 | 0.1986723 |
- Dos métodos full y subset
2.5.2 Metodo compelto
Para generar el estimador promedio de cada variable \(\hat{\theta}\), tomamos el valor del estimador de cada modelo \(i\) para esa variable (\(\theta_i\)) y posteriormente lo multiplicamos por el peso. La suma de estos productos es el nuevo estimador:
\[\hat{\theta} = \sum_{i=1}^R w_i \times \theta_i\]
Es importante que antes de hacer eso, tranfromemos los NA de los modelos en que no aparece la variable en ceros, esto lo hacemos con el siguiente código
S_full <- S %>% mutate(percentage.expenditure = case_when(is.na(percentage.expenditure) ~ 0,
!is.na(percentage.expenditure) ~ percentage.expenditure)) Para luego calcular los \(\theta_i\) de cada modelo con el siguiente código, con lo que obtenemos la tabla 2.2
| percentage.expenditure | weight | Theta_i |
|---|---|---|
| 0.00e+00 | 0.8013277 | 0.000000e+00 |
| 6.06e-05 | 0.1986723 | 1.204946e-05 |
Luego lo único que nos falta es sumar los valores calculados en la columna Theta_i.
Lo que nos dá un valor de 1.204946310^{-5}
2.5.3 Método subset
En el método subset, se hace un calculo similar, con la diferencia de que solo se utlizan los modelos en los cuales el parámetro se encuentra presente:
\[\hat{\theta} = \frac{\sum_{i=1}^Rw_i \times \theta_i}{\sum_{i=1}^Rw_i}\]
En este caso lo primero que debemos hacer es filtrar los modelos en que no se encuentra la variable percentage.expenditure:
Para luego multiplicar cada valor por su peso de akaike:
| percentage.expenditure | weight | Theta_i |
|---|---|---|
| 6.06e-05 | 0.1986723 | 1.204946e-05 |
Luego solo debemos sumar la columna Theta_i y dividirla por la suma de los pesos
para obtener un valor de 6.064992910^{-5}
2.5.4 Calculando los modelos promedios usando MuMIn
Para promediar modelos usando MuMIn, podemos usar la función moderl.avg, donde podemos generar el subset en la misma función:
Luego podemos ver para distintas variables sus parámetros promedio, en este caso mostraremos los del porcentaje de gastos y de enseñanza (Tabla 2.4):
| percentage.expenditure | Schooling | |
|---|---|---|
| full | 1.20e-05 | 0.1388644 |
| subset | 6.06e-05 | 0.1388644 |
2.5.5 Comparemos modelos
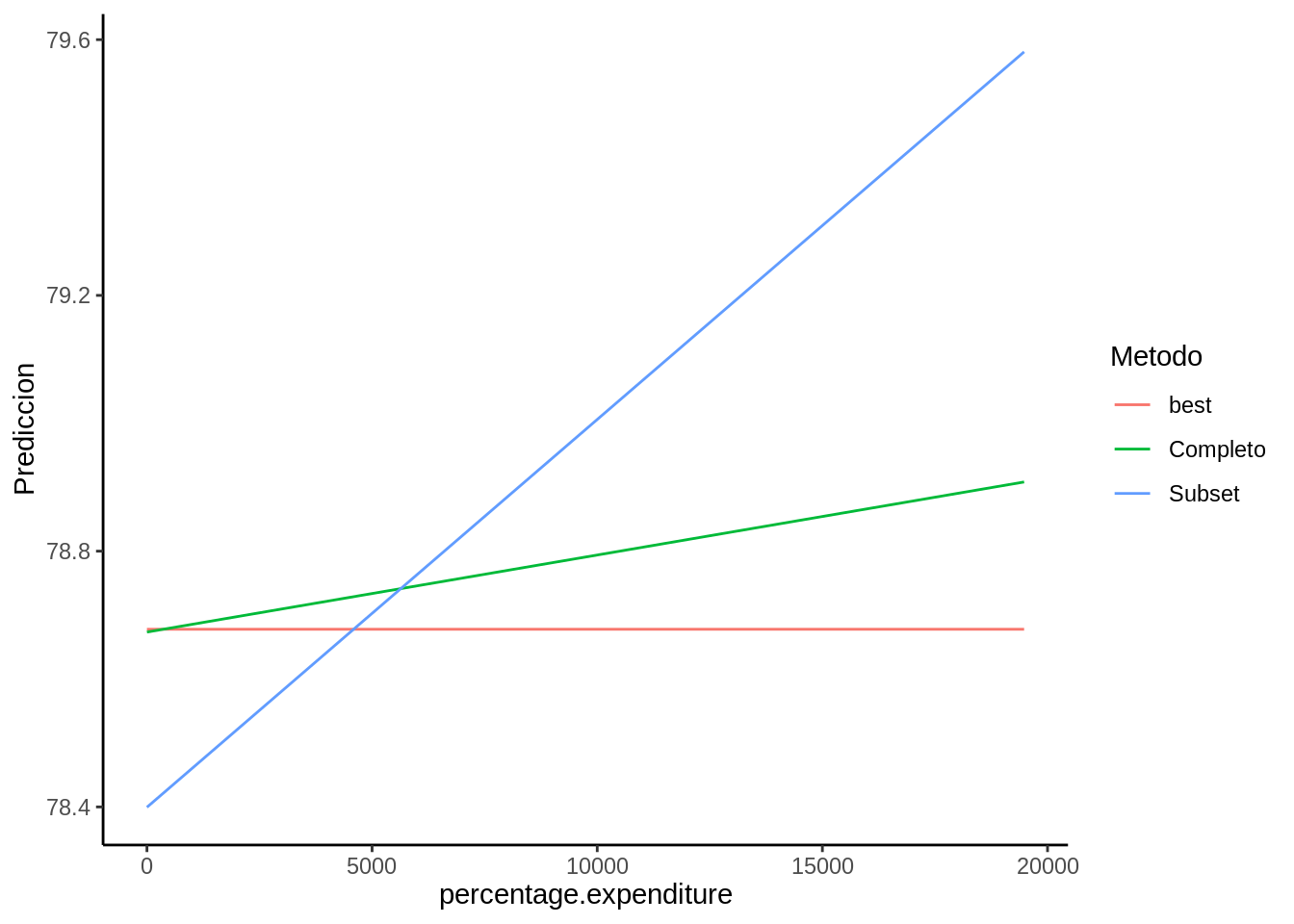
2.5.6 Comparemos modelos (cont.)
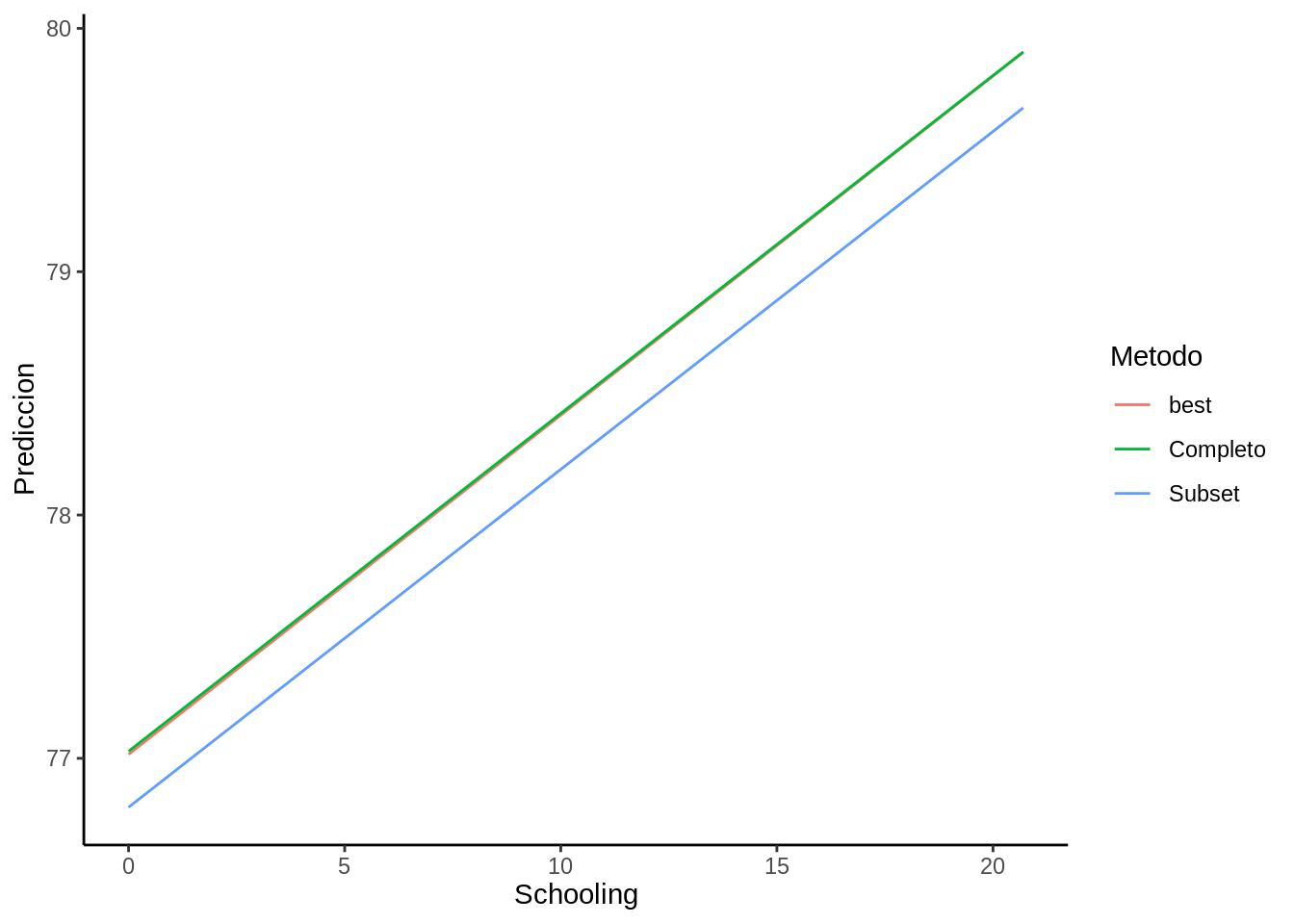
References
Anderson, D, and K Burnham. 2004. “Model Selection and Multi-Model Inference.” Second. NY: Springer-Verlag 63.
Bartoń, Kamil. 2019. MuMIn: Multi-Model Inference. https://CRAN.R-project.org/package=MuMIn.
Rajarshi, Kumar. 2018. “Life Expectancy (Who), Statistical Analysis on Factors Influencing Life Expectancy.” 2018.
Robinson, David, and Alex Hayes. 2020. Broom: Convert Statistical Analysis Objects into Tidy Tibbles. https://CRAN.R-project.org/package=broom.
Wickham, Hadley. 2019. Tidyverse: Easily Install and Load the ’Tidyverse’. https://CRAN.R-project.org/package=tidyverse.