Capítulo 4 Automatización de la seleccion de modelos

4.1 Paquetes necesarios para este capítulo

Para este capitulo necesitas tener instalado los paquetes tidyverse (Wickham 2019), broom (Robinson and Hayes 2020), lme4 (Bates et al. 2015) y MuMIn (Bartoń 2019)

4.1.1 Presentación html

Puedes seguir la clase de los videos en el siguiente link

y ver la clase en vivo desde las 20:30 horas el día martes 12 de Mayo del 2020 a continuación

Este video se cortó por falta de internet, acá esta la segunda parte

4.2 Variables fijas vs aleatorias

Tanto en los modelos lineales como en los GLM, siempre asumimos que todas las variables son fijas, esto es que toda variable tiene un efecto predecible y preciso de como afectará nuestro resultado final. Hoy introduciremos los modelos lineales mixtos y modelos generalizados mixtos, los cuales tienen variables fijas y aleatorias

Estas se definen a continuación:

Fijas (continuas o categóricas)
- Se espera que tengan una influencia predecible y sistemática en sobre lo que queremos explicar. Además, si es que son variables categóricas usan todos (o casi todos) los niveles de un factor (Ejemplo genero)
Aleatorias
- Se espera que su influencia sea impredecible e idiosincratica. Además no se usan todos los niveles de un factor (todos los individuos)

4.2.1 Ejemplo CO2

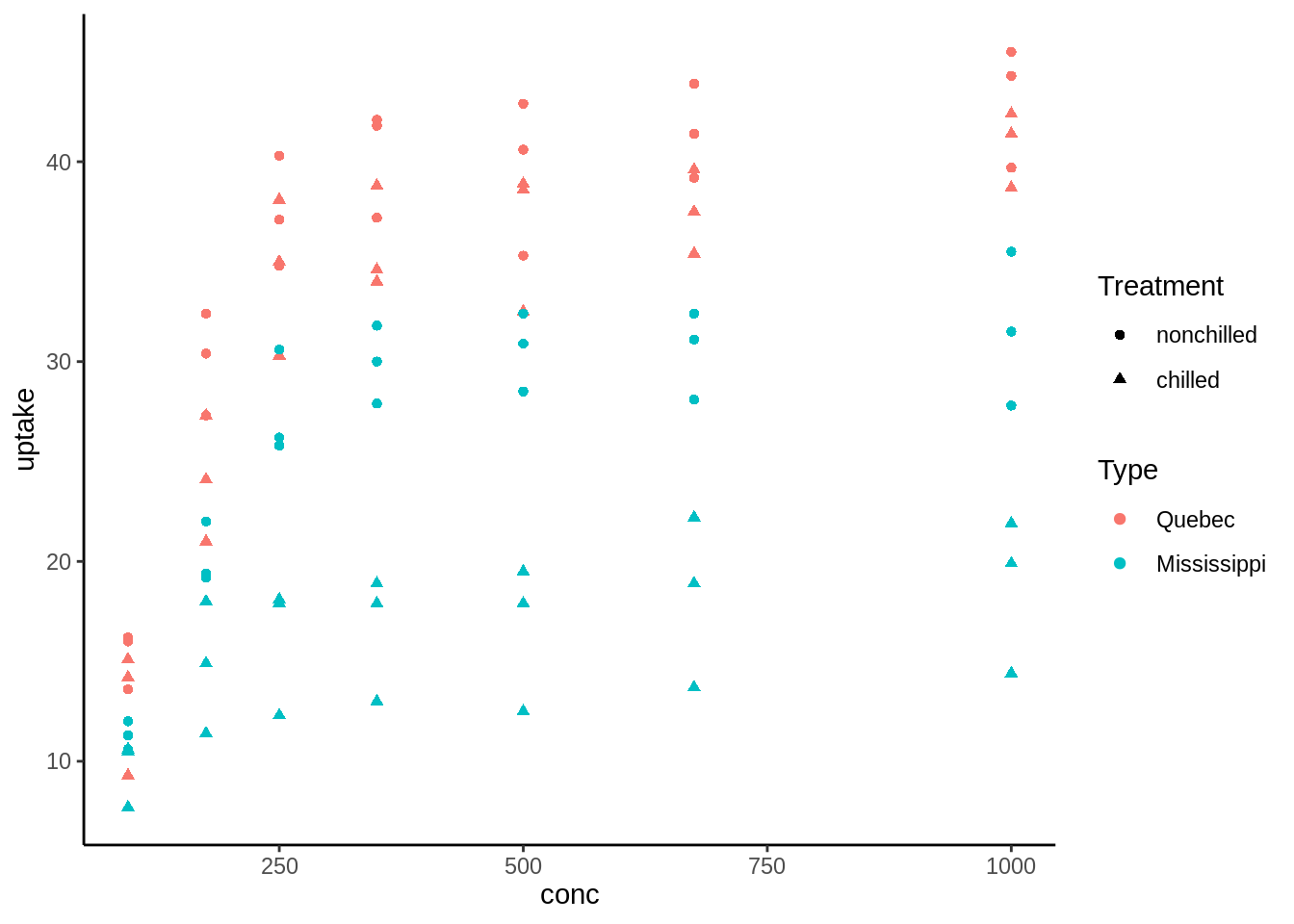
Para explicar los modelos lineales mixtos, usaremos una base de datos de un experimento con plantas de la misma especie (Potvin, Lechowicz, and Tardif 1990), la base de datos podemos verla entera en la tabla ?? y observar las relaciones en le figura ??. En este experimento distinas plantas fueron expuestas a distintas concentraciones de \(CO_2\), pero anteriormente fueron tratadas o no con temperaturas bajas. Este tratamiento está codificado en la columna Treatment. Además de esto tenemos que hay plantas provenientes de Mississippi y de Quebec y finalmente tenemos la identidad de las plantas en la variable Plant

Plant	Type	Treatment	conc	uptake
Qn1	Quebec	nonchilled	95	16.0
Qn1	Quebec	nonchilled	175	30.4
Qn1	Quebec	nonchilled	250	34.8
Qn1	Quebec	nonchilled	350	37.2
Qn1	Quebec	nonchilled	500	35.3
Qn1	Quebec	nonchilled	675	39.2
Qn1	Quebec	nonchilled	1000	39.7
Qn2	Quebec	nonchilled	95	13.6
Qn2	Quebec	nonchilled	175	27.3
Qn2	Quebec	nonchilled	250	37.1
Qn2	Quebec	nonchilled	350	41.8
Qn2	Quebec	nonchilled	500	40.6
Qn2	Quebec	nonchilled	675	41.4
Qn2	Quebec	nonchilled	1000	44.3
Qn3	Quebec	nonchilled	95	16.2
Qn3	Quebec	nonchilled	175	32.4
Qn3	Quebec	nonchilled	250	40.3
Qn3	Quebec	nonchilled	350	42.1
Qn3	Quebec	nonchilled	500	42.9
Qn3	Quebec	nonchilled	675	43.9
Qn3	Quebec	nonchilled	1000	45.5
Qc1	Quebec	chilled	95	14.2
Qc1	Quebec	chilled	175	24.1
Qc1	Quebec	chilled	250	30.3
Qc1	Quebec	chilled	350	34.6
Qc1	Quebec	chilled	500	32.5
Qc1	Quebec	chilled	675	35.4
Qc1	Quebec	chilled	1000	38.7
Qc2	Quebec	chilled	95	9.3
Qc2	Quebec	chilled	175	27.3
Qc2	Quebec	chilled	250	35.0
Qc2	Quebec	chilled	350	38.8
Qc2	Quebec	chilled	500	38.6
Qc2	Quebec	chilled	675	37.5
Qc2	Quebec	chilled	1000	42.4
Qc3	Quebec	chilled	95	15.1
Qc3	Quebec	chilled	175	21.0
Qc3	Quebec	chilled	250	38.1
Qc3	Quebec	chilled	350	34.0
Qc3	Quebec	chilled	500	38.9
Qc3	Quebec	chilled	675	39.6
Qc3	Quebec	chilled	1000	41.4
Mn1	Mississippi	nonchilled	95	10.6
Mn1	Mississippi	nonchilled	175	19.2
Mn1	Mississippi	nonchilled	250	26.2
Mn1	Mississippi	nonchilled	350	30.0
Mn1	Mississippi	nonchilled	500	30.9
Mn1	Mississippi	nonchilled	675	32.4
Mn1	Mississippi	nonchilled	1000	35.5
Mn2	Mississippi	nonchilled	95	12.0
Mn2	Mississippi	nonchilled	175	22.0
Mn2	Mississippi	nonchilled	250	30.6
Mn2	Mississippi	nonchilled	350	31.8
Mn2	Mississippi	nonchilled	500	32.4
Mn2	Mississippi	nonchilled	675	31.1
Mn2	Mississippi	nonchilled	1000	31.5
Mn3	Mississippi	nonchilled	95	11.3
Mn3	Mississippi	nonchilled	175	19.4
Mn3	Mississippi	nonchilled	250	25.8
Mn3	Mississippi	nonchilled	350	27.9
Mn3	Mississippi	nonchilled	500	28.5
Mn3	Mississippi	nonchilled	675	28.1
Mn3	Mississippi	nonchilled	1000	27.8
Mc1	Mississippi	chilled	95	10.5
Mc1	Mississippi	chilled	175	14.9
Mc1	Mississippi	chilled	250	18.1
Mc1	Mississippi	chilled	350	18.9
Mc1	Mississippi	chilled	500	19.5
Mc1	Mississippi	chilled	675	22.2
Mc1	Mississippi	chilled	1000	21.9
Mc2	Mississippi	chilled	95	7.7
Mc2	Mississippi	chilled	175	11.4
Mc2	Mississippi	chilled	250	12.3
Mc2	Mississippi	chilled	350	13.0
Mc2	Mississippi	chilled	500	12.5
Mc2	Mississippi	chilled	675	13.7
Mc2	Mississippi	chilled	1000	14.4
Mc3	Mississippi	chilled	95	10.6
Mc3	Mississippi	chilled	175	18.0
Mc3	Mississippi	chilled	250	17.9
Mc3	Mississippi	chilled	350	17.9
Mc3	Mississippi	chilled	500	17.9
Mc3	Mississippi	chilled	675	18.9
Mc3	Mississippi	chilled	1000	19.9

Partiremos con un ejemplo de un modelo lineal y un modelo lineal mixto en paralelo para empezar a trabajar. El modelo codificado como mod1 es un modelo lineal, en el cual asumimos que existirá un comportamiento logarítmico de la captación de \(CO2\), esto es, se saturará la relación

library(lme4)
mod1 <- lm(uptake ~ Type * Treatment + I(log(conc)) + conc, data = CO2)
mod2 <- lmer(uptake ~ Type * Treatment + I(log(conc)) + conc + (1 | Plant), data = CO2)

options(na.action = "na.fail")
Max.Vars <- floor(nrow(CO2)/10)
Seleccion <- dredge(mod2, m.lim = c(0, Max.Vars))

4.2.2 Selección

(Intercept)	conc	I(log(conc))	Treatment	Type	Treatment:Type	df	logLik	AICc	delta	weight
-57.247	-0.025	17.789				8	-230.705	479.331	0.000	0.963
-55.608	-0.025	17.789			NA	7	-235.188	485.850	6.519	0.037
-59.037	-0.025	17.789	NA		NA	6	-241.972	497.036	17.705	0.000
-14.037	NA	8.484				7	-241.168	497.809	18.478	0.000
-12.398	NA	8.484			NA	6	-245.650	504.392	25.061	0.000
-61.937	-0.025	17.789		NA	NA	6	-246.728	506.546	27.215	0.000
-65.367	-0.025	17.789	NA	NA	NA	5	-250.329	511.428	32.097	0.000
-15.827	NA	8.484	NA		NA	5	-252.435	515.638	36.307	0.000
-18.727	NA	8.484		NA	NA	5	-257.190	525.149	45.818	0.000
-22.157	NA	8.484	NA	NA	NA	4	-260.792	530.089	50.759	0.000
27.621	0.018	NA				7	-267.614	550.702	71.371	0.000
29.260	0.018	NA			NA	6	-272.096	557.284	77.953	0.000
25.830	0.018	NA	NA		NA	5	-278.881	568.530	89.200	0.000
22.930	0.018	NA		NA	NA	5	-283.636	578.041	98.710	0.000
19.500	0.018	NA	NA	NA	NA	4	-287.238	582.982	103.651	0.000
35.333	NA	NA				6	-286.019	585.128	105.798	0.000
36.973	NA	NA			NA	5	-289.930	590.630	111.299	0.000
33.543	NA	NA	NA		NA	4	-296.656	601.819	122.488	0.000
30.643	NA	NA		NA	NA	4	-301.412	611.330	131.999	0.000
27.213	NA	NA	NA	NA	NA	3	-305.013	616.327	136.996	0.000

Solo el primer modelo es seleccionado

4.2.3 Modelo

BestModel <- get.models(Seleccion, 1)[[1]]
broom::tidy(BestModel)

term	estimate	std.error	statistic	group
(Intercept)	-57.247	7.867	-7.277	fixed
conc	-0.025	0.004	-6.075	fixed
I(log(conc))	17.789	1.622	10.970	fixed
Treatmentchilled	-3.581	1.835	-1.952	fixed
TypeMississippi	-9.381	1.835	-5.112	fixed
Treatmentchilled:TypeMississippi	-6.557	2.595	-2.527	fixed
sd_(Intercept).Plant	1.769	NA	NA	Plant
sd_Observation.Residual	3.667	NA	NA	Residual

4.2.4 Modelo

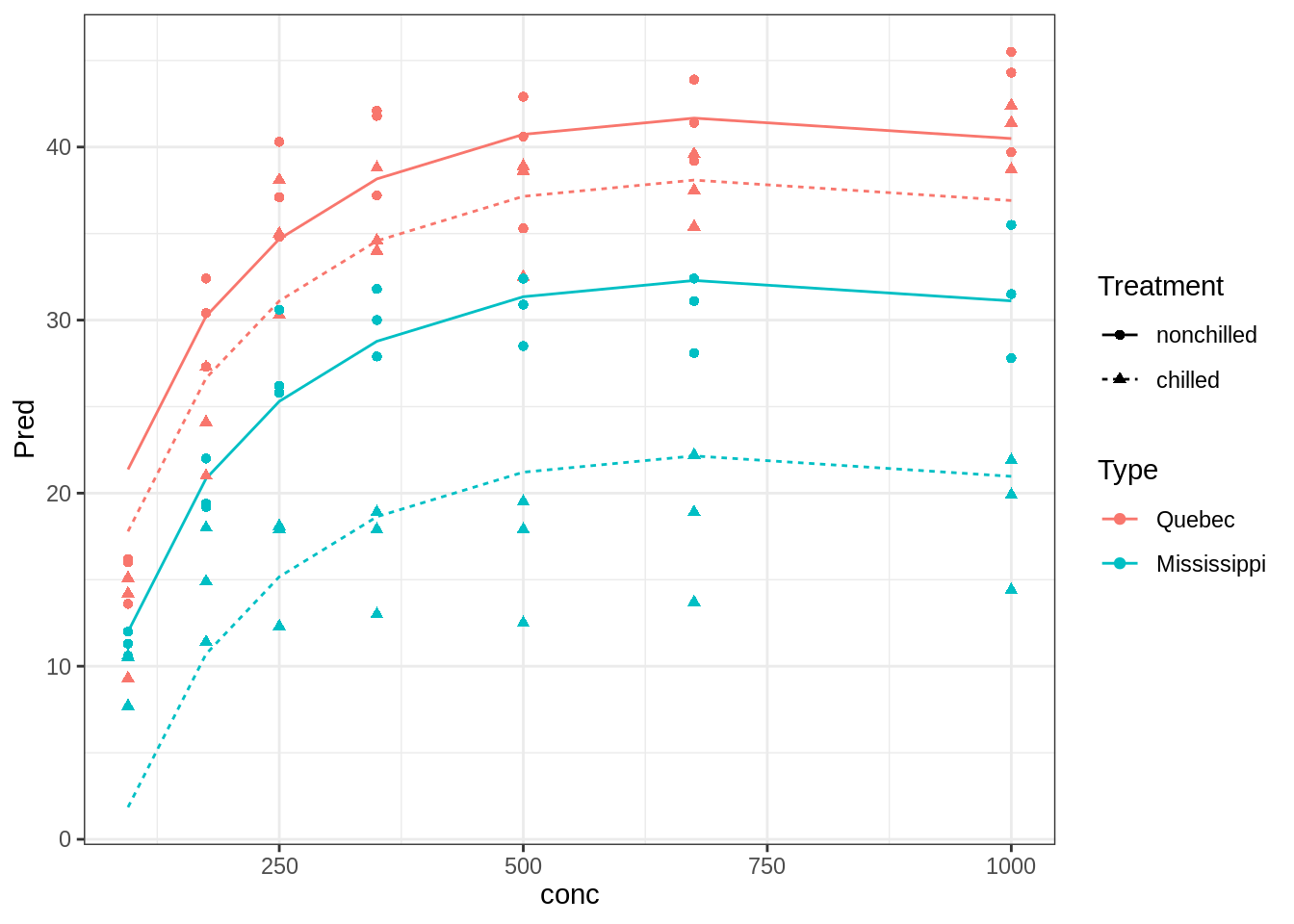
4.2.4.1 Cemento

¿Que problema tiene la siguiente base de datos para LMs o GLMs?
Ejemplo base de datos Cement de MuMIn

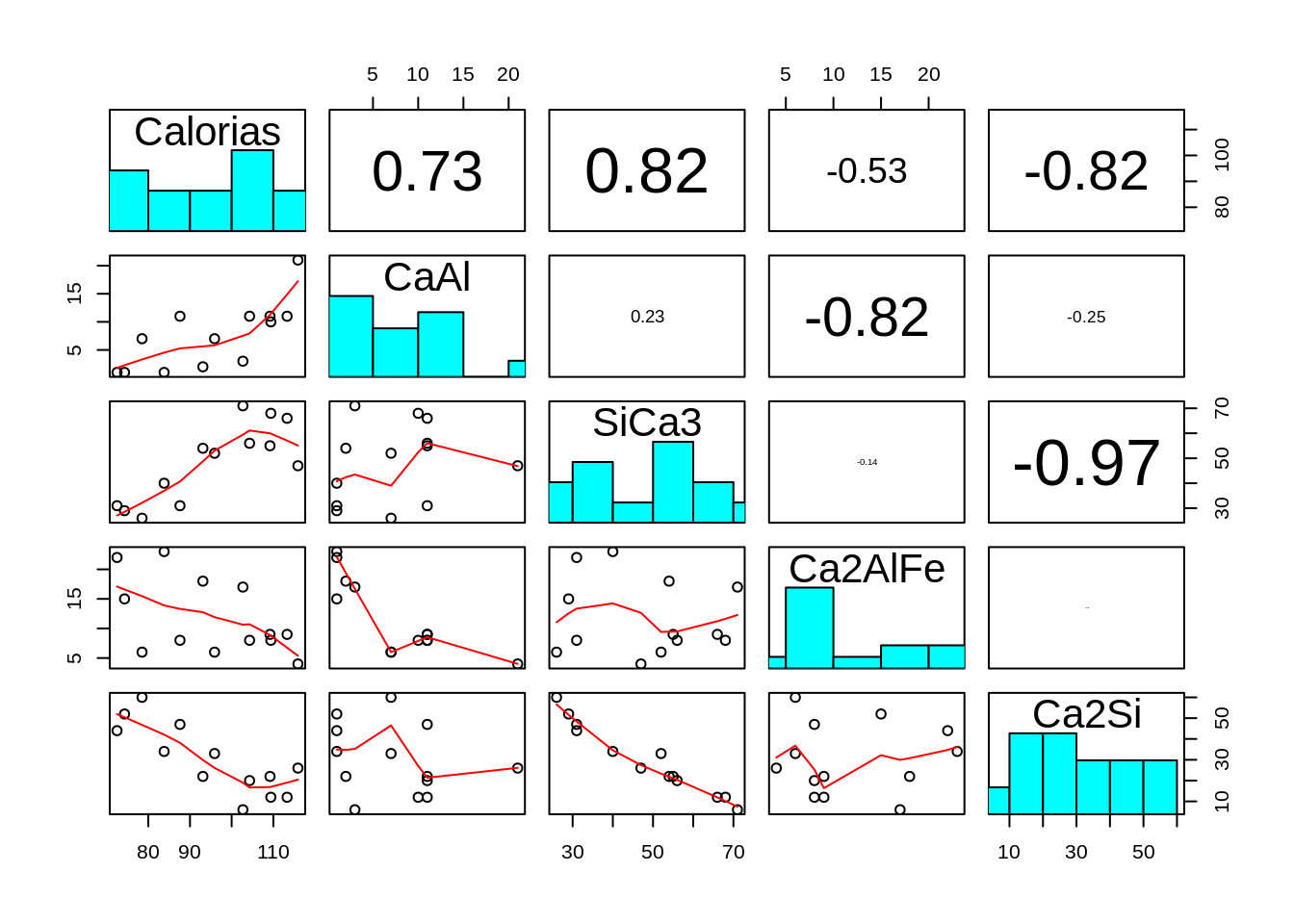
4.2.5 Como agrego eso a MuMIn

GlobalMod <- lm(Calorias ~ ., data = Cement2)

cor(Cement2[, -1])

	CaAl	SiCa3	Ca2AlFe	Ca2Si
CaAl	1.0000000	0.2285795	-0.8241338	-0.2454451
SiCa3	0.2285795	1.0000000	-0.1392424	-0.9729550
Ca2AlFe	-0.8241338	-0.1392424	1.0000000	0.0295370
Ca2Si	-0.2454451	-0.9729550	0.0295370	1.0000000

nm <- colnames(Cement2[-1])
smat <- abs(cor(Cement2[, -1])) <= 0.7
smat[!lower.tri(smat)] <- NA

	CaAl	SiCa3	Ca2AlFe	Ca2Si
CaAl	NA	NA	NA	NA
SiCa3	TRUE	NA	NA	NA
Ca2AlFe	FALSE	TRUE	NA	NA
Ca2Si	TRUE	FALSE	TRUE	NA

options(na.action = "na.fail")
Selected <- dredge(GlobalMod, subset = smat)

(Intercept)	Ca2AlFe	Ca2Si	CaAl	SiCa3	df	logLik	AICc	delta	weight
52.58	NA	NA	1.47	0.66	4	-28.16	69.31	0.00	0.84
103.10	NA	-0.61	1.44	NA	4	-29.82	72.63	3.32	0.16
131.28	-1.20	-0.72	NA	NA	4	-35.37	83.74	14.43	0.00
72.07	-1.01	NA	NA	0.73	4	-40.96	94.93	25.62	0.00
117.57	NA	-0.74	NA	NA	3	-45.87	100.41	31.10	0.00
57.42	NA	NA	NA	0.79	3	-46.04	100.74	31.42	0.00
81.48	NA	NA	1.87	NA	3	-48.21	105.08	35.77	0.00
110.20	-1.26	NA	NA	NA	3	-50.98	110.63	41.31	0.00
95.42	NA	NA	NA	NA	2	-53.17	111.54	42.22	0.00

4.3 Incluir además límite de numero de variables

options(na.action = "na.fail")
Selected <- dredge(GlobalMod, subset = smat, m.lim = c(0, floor(nrow(Cement)/10)))

(Intercept)	Ca2AlFe	Ca2Si	CaAl	SiCa3	df	logLik	AICc	delta	weight
117.57	NA	-0.74	NA	NA	3	-45.87	100.41	0.00	0.51
57.42	NA	NA	NA	0.79	3	-46.04	100.74	0.33	0.43
81.48	NA	NA	1.87	NA	3	-48.21	105.08	4.67	0.05
110.20	-1.26	NA	NA	NA	3	-50.98	110.63	10.22	0.00
95.42	NA	NA	NA	NA	2	-53.17	111.54	11.13	0.00

4.4 Preguntas

4.4.1 Pregunta 1

¿Cual de estas relaciones es la que uno esperaría ver al finalizar el experimento?

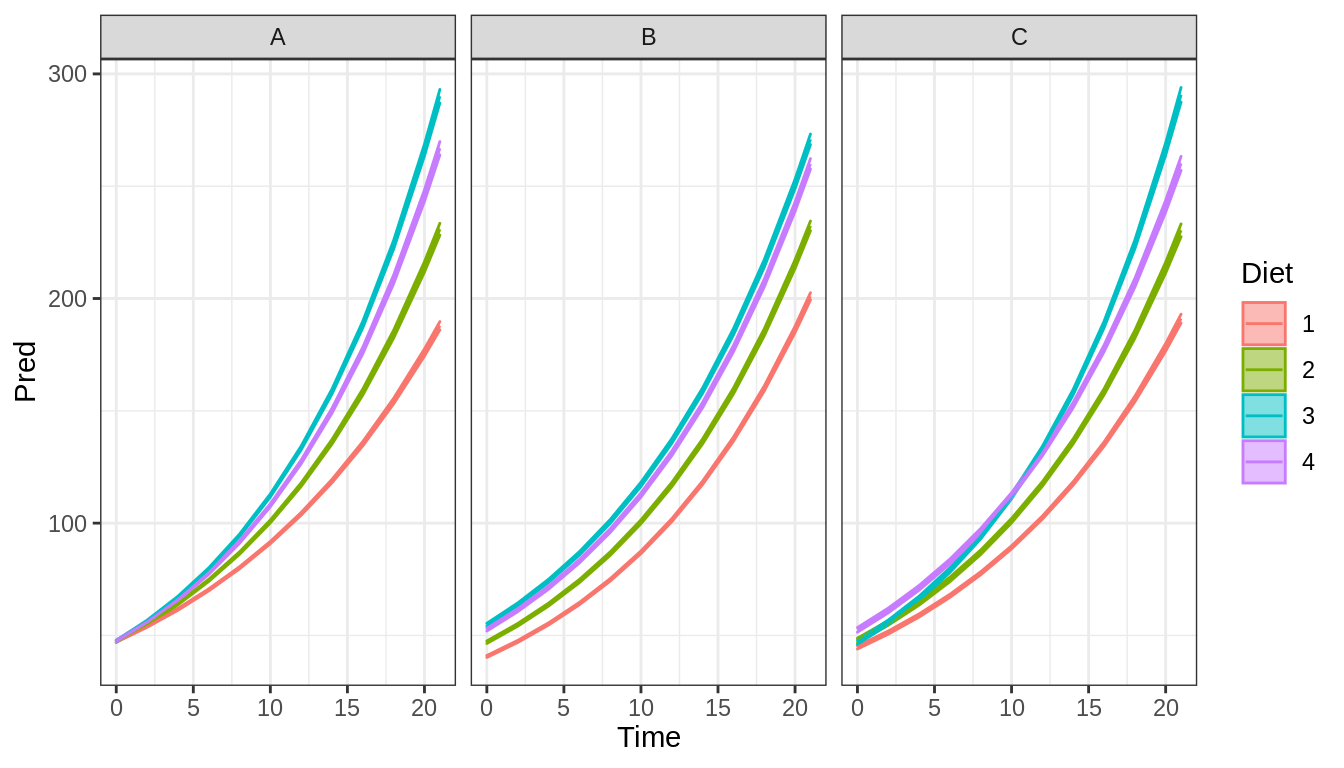
00:40

Respuesta: A

4.4.2 Pregunta 2

¿Cuál de estos códigos resultaría en el modelo que generaría este gráfico?

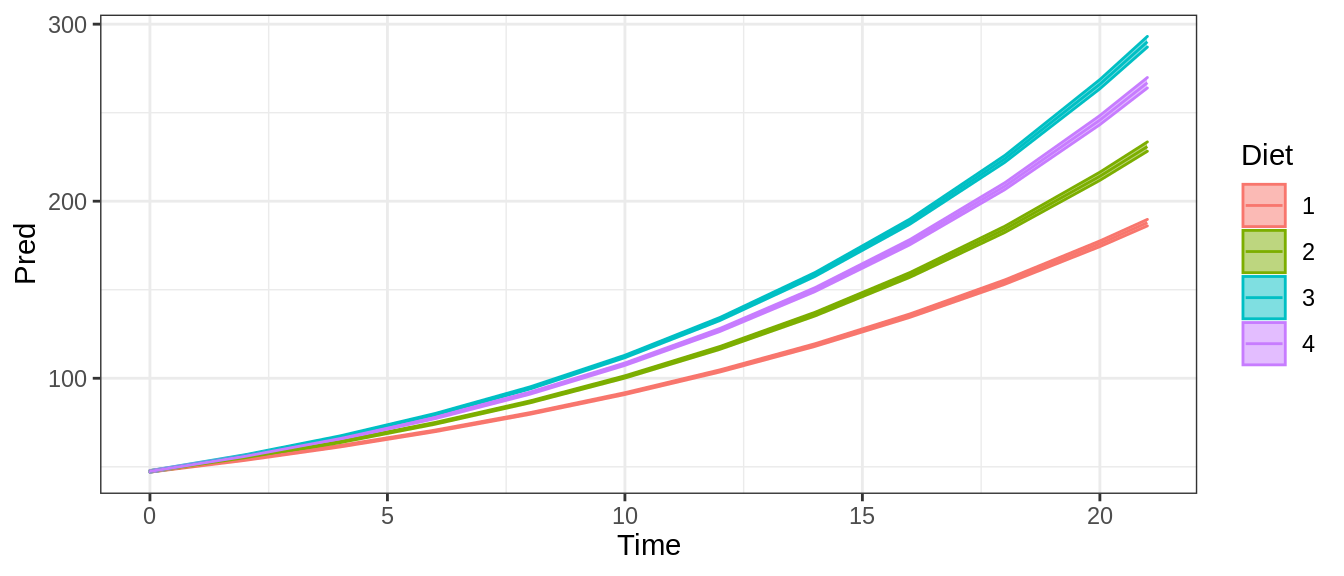
A <- glm(weight ~ Time + Diet, family = poisson)
B <- glm(weight ~ Time * Diet, family = poisson)
C <- glm(weight ~ Time + Time:Diet, family = poisson)

00:40

library(lme4)
ChickPoissMM1 <- glmer(weight ~ Time + Diet + (1 | Chick), family = poisson, 
    data = ChickWeight)
ChickPoissMM2 <- glmer(weight ~ Time + Time:Diet + (1 | Chick), 
    family = poisson, data = ChickWeight)
ChickPoissMM3 <- glmer(weight ~ Time + Time * Diet + (1 | Chick), 
    family = poisson, data = ChickWeight)

4.4.3 Pregunta 3

¿Cuanto pesaria un pollo en el dia 10 en la dieta 2 basado en el modelo anterior?

term	estimate	std.error	statistic	p.value	group
(Intercept)	3.84	0.03	121.74	0	fixed
Time	0.07	0.00	63.72	0	fixed
Time:Diet2	0.01	0.00	4.99	0	fixed
Time:Diet3	0.02	0.00	12.59	0	fixed
Time:Diet4	0.01	0.00	5.91	0	fixed
sd_(Intercept).Chick	0.21	NA	NA	NA	Chick

A = 94.6324083
B = 113.2955623
C = 4.73

00:40

exp(3.83 + 10 * 0.07 + 0.02)

## [1] 94.63241

exp(3.83 + 10 * 0.07 + (10 * 0.02))

## [1] 113.2956

3.83 + 10 * 0.07 + (10 * 0.02)

## [1] 4.73

4.4.4 Pregunta 4

¿Cuál es el código que mejor representa este gráfico?

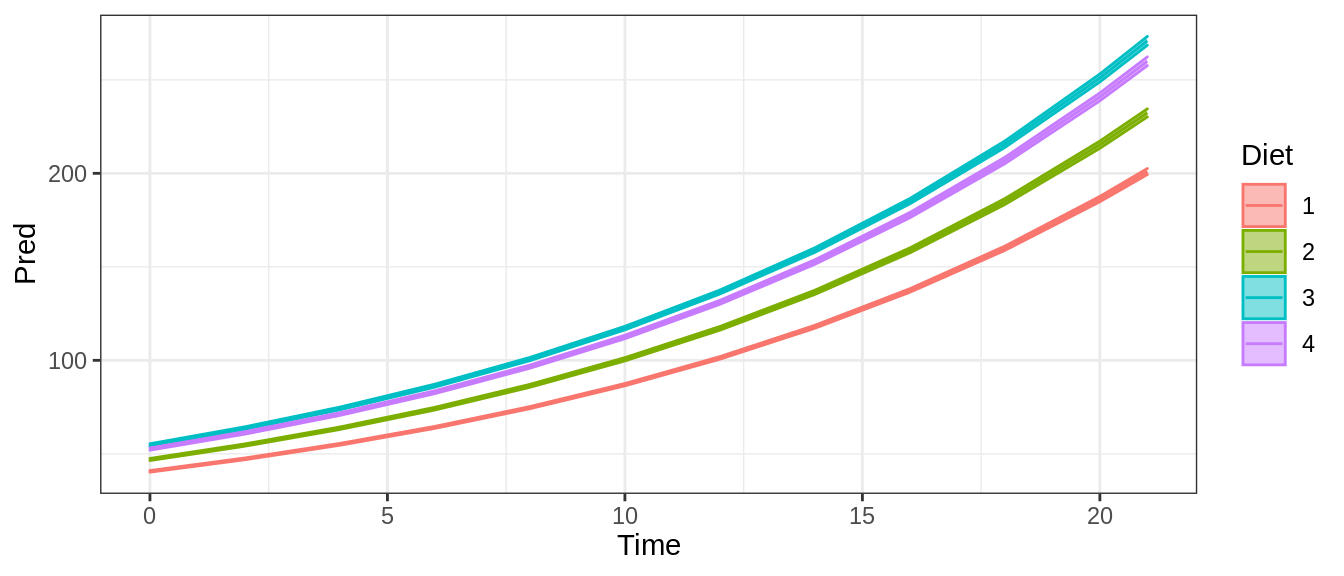
A <- glm(weight ~ Time + Diet, family = poisson)
B <- glm(weight ~ Time * Diet, family = poisson)
C <- glm(weight ~ Time + Time:Diet, family = poisson)

00:40

4.4.5 Pregunta 5

¿Cuantas pendientes e interceptos espero ver en este modelo?

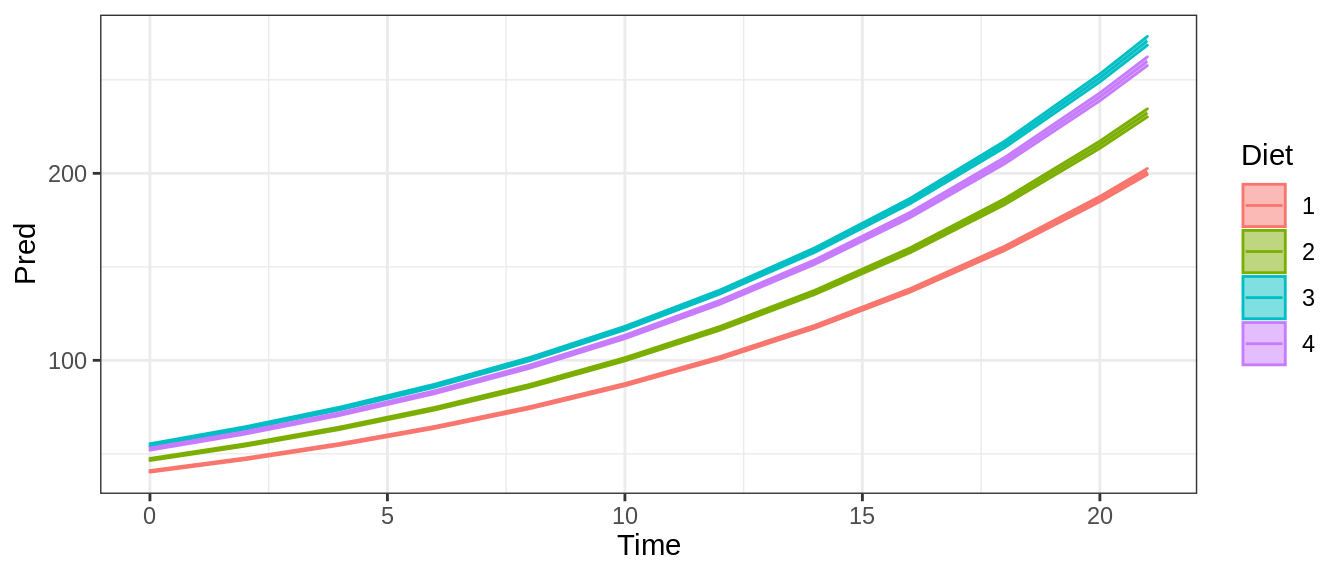
00:40

term	estimate	std.error	statistic
(Intercept)	3.70	0.01	346.30
Time	0.08	0.00	125.25
Diet2	0.15	0.01	13.69
Diet3	0.30	0.01	29.46
Diet4	0.26	0.01	24.88

References

Bartoń, Kamil. 2019. MuMIn: Multi-Model Inference. https://CRAN.R-project.org/package=MuMIn.

Bates, Douglas, Martin Mächler, Ben Bolker, and Steve Walker. 2015. “Fitting Linear Mixed-Effects Models Using lme4.” Journal of Statistical Software 67 (1): 1–48. https://doi.org/10.18637/jss.v067.i01.

Potvin, Catherine, Martin J Lechowicz, and Serge Tardif. 1990. “The Statistical Analysis of Ecophysiological Response Curves Obtained from Experiments Involving Repeated Measures.” Ecology 71 (4). Wiley Online Library: 1389–1400.

Robinson, David, and Alex Hayes. 2020. Broom: Convert Statistical Analysis Objects into Tidy Tibbles. https://CRAN.R-project.org/package=broom.

Wickham, Hadley. 2019. Tidyverse: Easily Install and Load the ’Tidyverse’. https://CRAN.R-project.org/package=tidyverse.