- Algoritmos de inteligencia artificial
- Perfectos para máxima predicción
- En general malos para explicar
- El mejor caso es cuando tengo al menos 1000 casos
- Si tengo millones de datos, mejor deeplearning
- Tanto para clasificación como regresión
19/05, 2020
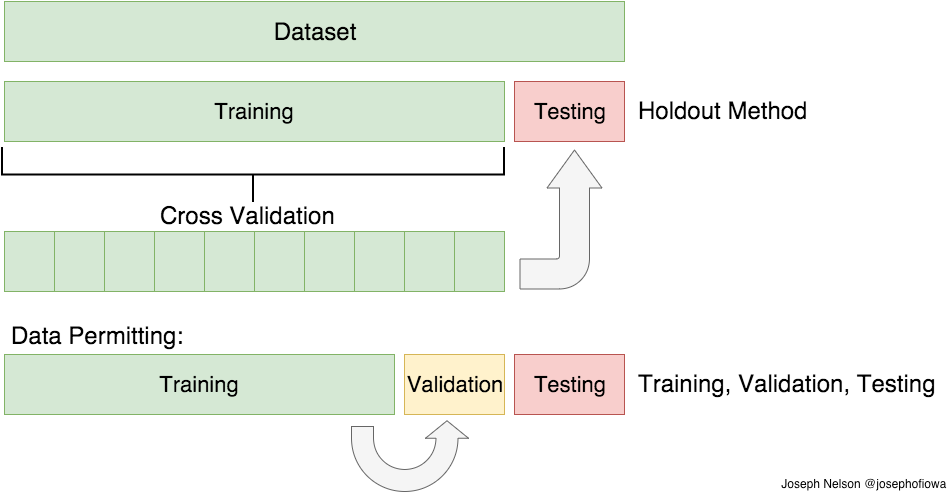
Machine learning (que es y cuando usarlo)
En general Crossvalidation
Partamos con clasificación
| Sepal.Length | Sepal.Width | Petal.Length | Petal.Width | Species |
|---|---|---|---|---|
| 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 5.0 | 3.6 | 1.4 | 0.2 | setosa |
| 5.4 | 3.9 | 1.7 | 0.4 | setosa |
| 4.6 | 3.4 | 1.4 | 0.3 | setosa |
| 5.0 | 3.4 | 1.5 | 0.2 | setosa |
| 4.4 | 2.9 | 1.4 | 0.2 | setosa |
| 4.9 | 3.1 | 1.5 | 0.1 | setosa |
| 5.4 | 3.7 | 1.5 | 0.2 | setosa |
| 4.8 | 3.4 | 1.6 | 0.2 | setosa |
| 4.8 | 3.0 | 1.4 | 0.1 | setosa |
| 4.3 | 3.0 | 1.1 | 0.1 | setosa |
| 5.8 | 4.0 | 1.2 | 0.2 | setosa |
| 5.7 | 4.4 | 1.5 | 0.4 | setosa |
| 5.4 | 3.9 | 1.3 | 0.4 | setosa |
| 5.1 | 3.5 | 1.4 | 0.3 | setosa |
| 5.7 | 3.8 | 1.7 | 0.3 | setosa |
| 5.1 | 3.8 | 1.5 | 0.3 | setosa |
| 5.4 | 3.4 | 1.7 | 0.2 | setosa |
| 5.1 | 3.7 | 1.5 | 0.4 | setosa |
| 4.6 | 3.6 | 1.0 | 0.2 | setosa |
| 5.1 | 3.3 | 1.7 | 0.5 | setosa |
| 4.8 | 3.4 | 1.9 | 0.2 | setosa |
| 5.0 | 3.0 | 1.6 | 0.2 | setosa |
| 5.0 | 3.4 | 1.6 | 0.4 | setosa |
| 5.2 | 3.5 | 1.5 | 0.2 | setosa |
| 5.2 | 3.4 | 1.4 | 0.2 | setosa |
| 4.7 | 3.2 | 1.6 | 0.2 | setosa |
| 4.8 | 3.1 | 1.6 | 0.2 | setosa |
| 5.4 | 3.4 | 1.5 | 0.4 | setosa |
| 5.2 | 4.1 | 1.5 | 0.1 | setosa |
| 5.5 | 4.2 | 1.4 | 0.2 | setosa |
| 4.9 | 3.1 | 1.5 | 0.2 | setosa |
| 5.0 | 3.2 | 1.2 | 0.2 | setosa |
| 5.5 | 3.5 | 1.3 | 0.2 | setosa |
| 4.9 | 3.6 | 1.4 | 0.1 | setosa |
| 4.4 | 3.0 | 1.3 | 0.2 | setosa |
| 5.1 | 3.4 | 1.5 | 0.2 | setosa |
| 5.0 | 3.5 | 1.3 | 0.3 | setosa |
| 4.5 | 2.3 | 1.3 | 0.3 | setosa |
| 4.4 | 3.2 | 1.3 | 0.2 | setosa |
| 5.0 | 3.5 | 1.6 | 0.6 | setosa |
| 5.1 | 3.8 | 1.9 | 0.4 | setosa |
| 4.8 | 3.0 | 1.4 | 0.3 | setosa |
| 5.1 | 3.8 | 1.6 | 0.2 | setosa |
| 4.6 | 3.2 | 1.4 | 0.2 | setosa |
| 5.3 | 3.7 | 1.5 | 0.2 | setosa |
| 5.0 | 3.3 | 1.4 | 0.2 | setosa |
| 7.0 | 3.2 | 4.7 | 1.4 | versicolor |
| 6.4 | 3.2 | 4.5 | 1.5 | versicolor |
| 6.9 | 3.1 | 4.9 | 1.5 | versicolor |
| 5.5 | 2.3 | 4.0 | 1.3 | versicolor |
| 6.5 | 2.8 | 4.6 | 1.5 | versicolor |
| 5.7 | 2.8 | 4.5 | 1.3 | versicolor |
| 6.3 | 3.3 | 4.7 | 1.6 | versicolor |
| 4.9 | 2.4 | 3.3 | 1.0 | versicolor |
| 6.6 | 2.9 | 4.6 | 1.3 | versicolor |
| 5.2 | 2.7 | 3.9 | 1.4 | versicolor |
| 5.0 | 2.0 | 3.5 | 1.0 | versicolor |
| 5.9 | 3.0 | 4.2 | 1.5 | versicolor |
| 6.0 | 2.2 | 4.0 | 1.0 | versicolor |
| 6.1 | 2.9 | 4.7 | 1.4 | versicolor |
| 5.6 | 2.9 | 3.6 | 1.3 | versicolor |
| 6.7 | 3.1 | 4.4 | 1.4 | versicolor |
| 5.6 | 3.0 | 4.5 | 1.5 | versicolor |
| 5.8 | 2.7 | 4.1 | 1.0 | versicolor |
| 6.2 | 2.2 | 4.5 | 1.5 | versicolor |
| 5.6 | 2.5 | 3.9 | 1.1 | versicolor |
| 5.9 | 3.2 | 4.8 | 1.8 | versicolor |
| 6.1 | 2.8 | 4.0 | 1.3 | versicolor |
| 6.3 | 2.5 | 4.9 | 1.5 | versicolor |
| 6.1 | 2.8 | 4.7 | 1.2 | versicolor |
| 6.4 | 2.9 | 4.3 | 1.3 | versicolor |
| 6.6 | 3.0 | 4.4 | 1.4 | versicolor |
| 6.8 | 2.8 | 4.8 | 1.4 | versicolor |
| 6.7 | 3.0 | 5.0 | 1.7 | versicolor |
| 6.0 | 2.9 | 4.5 | 1.5 | versicolor |
| 5.7 | 2.6 | 3.5 | 1.0 | versicolor |
| 5.5 | 2.4 | 3.8 | 1.1 | versicolor |
| 5.5 | 2.4 | 3.7 | 1.0 | versicolor |
| 5.8 | 2.7 | 3.9 | 1.2 | versicolor |
| 6.0 | 2.7 | 5.1 | 1.6 | versicolor |
| 5.4 | 3.0 | 4.5 | 1.5 | versicolor |
| 6.0 | 3.4 | 4.5 | 1.6 | versicolor |
| 6.7 | 3.1 | 4.7 | 1.5 | versicolor |
| 6.3 | 2.3 | 4.4 | 1.3 | versicolor |
| 5.6 | 3.0 | 4.1 | 1.3 | versicolor |
| 5.5 | 2.5 | 4.0 | 1.3 | versicolor |
| 5.5 | 2.6 | 4.4 | 1.2 | versicolor |
| 6.1 | 3.0 | 4.6 | 1.4 | versicolor |
| 5.8 | 2.6 | 4.0 | 1.2 | versicolor |
| 5.0 | 2.3 | 3.3 | 1.0 | versicolor |
| 5.6 | 2.7 | 4.2 | 1.3 | versicolor |
| 5.7 | 3.0 | 4.2 | 1.2 | versicolor |
| 5.7 | 2.9 | 4.2 | 1.3 | versicolor |
| 6.2 | 2.9 | 4.3 | 1.3 | versicolor |
| 5.1 | 2.5 | 3.0 | 1.1 | versicolor |
| 5.7 | 2.8 | 4.1 | 1.3 | versicolor |
| 6.3 | 3.3 | 6.0 | 2.5 | virginica |
| 5.8 | 2.7 | 5.1 | 1.9 | virginica |
| 7.1 | 3.0 | 5.9 | 2.1 | virginica |
| 6.3 | 2.9 | 5.6 | 1.8 | virginica |
| 6.5 | 3.0 | 5.8 | 2.2 | virginica |
| 7.6 | 3.0 | 6.6 | 2.1 | virginica |
| 4.9 | 2.5 | 4.5 | 1.7 | virginica |
| 7.3 | 2.9 | 6.3 | 1.8 | virginica |
| 6.7 | 2.5 | 5.8 | 1.8 | virginica |
| 7.2 | 3.6 | 6.1 | 2.5 | virginica |
| 6.5 | 3.2 | 5.1 | 2.0 | virginica |
| 6.4 | 2.7 | 5.3 | 1.9 | virginica |
| 6.8 | 3.0 | 5.5 | 2.1 | virginica |
| 5.7 | 2.5 | 5.0 | 2.0 | virginica |
| 5.8 | 2.8 | 5.1 | 2.4 | virginica |
| 6.4 | 3.2 | 5.3 | 2.3 | virginica |
| 6.5 | 3.0 | 5.5 | 1.8 | virginica |
| 7.7 | 3.8 | 6.7 | 2.2 | virginica |
| 7.7 | 2.6 | 6.9 | 2.3 | virginica |
| 6.0 | 2.2 | 5.0 | 1.5 | virginica |
| 6.9 | 3.2 | 5.7 | 2.3 | virginica |
| 5.6 | 2.8 | 4.9 | 2.0 | virginica |
| 7.7 | 2.8 | 6.7 | 2.0 | virginica |
| 6.3 | 2.7 | 4.9 | 1.8 | virginica |
| 6.7 | 3.3 | 5.7 | 2.1 | virginica |
| 7.2 | 3.2 | 6.0 | 1.8 | virginica |
| 6.2 | 2.8 | 4.8 | 1.8 | virginica |
| 6.1 | 3.0 | 4.9 | 1.8 | virginica |
| 6.4 | 2.8 | 5.6 | 2.1 | virginica |
| 7.2 | 3.0 | 5.8 | 1.6 | virginica |
| 7.4 | 2.8 | 6.1 | 1.9 | virginica |
| 7.9 | 3.8 | 6.4 | 2.0 | virginica |
| 6.4 | 2.8 | 5.6 | 2.2 | virginica |
| 6.3 | 2.8 | 5.1 | 1.5 | virginica |
| 6.1 | 2.6 | 5.6 | 1.4 | virginica |
| 7.7 | 3.0 | 6.1 | 2.3 | virginica |
| 6.3 | 3.4 | 5.6 | 2.4 | virginica |
| 6.4 | 3.1 | 5.5 | 1.8 | virginica |
| 6.0 | 3.0 | 4.8 | 1.8 | virginica |
| 6.9 | 3.1 | 5.4 | 2.1 | virginica |
| 6.7 | 3.1 | 5.6 | 2.4 | virginica |
| 6.9 | 3.1 | 5.1 | 2.3 | virginica |
| 5.8 | 2.7 | 5.1 | 1.9 | virginica |
| 6.8 | 3.2 | 5.9 | 2.3 | virginica |
| 6.7 | 3.3 | 5.7 | 2.5 | virginica |
| 6.7 | 3.0 | 5.2 | 2.3 | virginica |
| 6.3 | 2.5 | 5.0 | 1.9 | virginica |
| 6.5 | 3.0 | 5.2 | 2.0 | virginica |
| 6.2 | 3.4 | 5.4 | 2.3 | virginica |
| 5.9 | 3.0 | 5.1 | 1.8 | virginica |
Caracteres buenos para clasificar
Caracteres malos para clasificar
Usemos caret!!!!
- Lo primero dividir en Entrenamiento y Prueba
set.seed(2020) Index <- createDataPartition(iris$Species, list = FALSE, p = 0.5) Train <- iris[Index, ] Test <- iris[-Index, ]
- Luego preparo el entrenamiento 10 fold repeated Crossvalidation
fitControl <- trainControl(method = "repeatedcv", number = 10, repeats = 10)
¿Repeated que?
Elegimos un algorítmo
| X1 | Classification | Regression | Accepts Case Weights | Bagging | Bayesian Model | Binary Predictors Only | Boosting | Categorical Predictors Only | Cost Sensitive Learning | Discriminant Analysis | Discriminant Analysis Models | Distance Weighted Discrimination | Ensemble Model | Feature Extraction | Feature Extraction Models | Feature Selection Wrapper | Gaussian Process | Generalized Additive Model | Generalized Linear Model | Generalized Linear Models | Handle Missing Predictor Data | Implicit Feature Selection | Kernel Method | L1 Regularization | L1 Regularization Models | L2 Regularization | L2 Regularization Models | Linear Classifier | Linear Classifier Models | Linear Regression | Linear Regression Models | Logic Regression | Logistic Regression | Mixture Model | Model Tree | Multivariate Adaptive Regression Splines | Neural Network | Oblique Tree | Ordinal Outcomes | Partial Least Squares | Patient Rule Induction Method | Polynomial Model | Prototype Models | Quantile Regression | Radial Basis Function | Random Forest | Regularization | Relevance Vector Machines | Ridge Regression | Robust Methods | Robust Model | ROC Curves | Rule-Based Model | Self-Organising Maps | String Kernel | Support Vector Machines | Text Mining | Tree-Based Model | Two Class Only |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Boosted Classification Trees (ada) | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| Bagged AdaBoost (AdaBag) | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| AdaBoost.M1 (AdaBoost.M1) | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| AdaBoost Classification Trees (adaboost) | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| Adaptive Mixture Discriminant Analysis (amdai) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Adaptive-Network-Based Fuzzy Inference System (ANFIS) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Model Averaged Neural Network (avNNet) | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Naive Bayes Classifier with Attribute Weighting (awnb) | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Tree Augmented Naive Bayes Classifier with Attribute Weighting (awtan) | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bagged Model (bag) | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bagged MARS (bagEarth) | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bagged MARS using gCV Pruning (bagEarthGCV) | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bagged Flexible Discriminant Analysis (bagFDA) | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bagged FDA using gCV Pruning (bagFDAGCV) | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Generalized Additive Model using Splines (bam) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bayesian Additive Regression Trees (bartMachine) | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| Bayesian Generalized Linear Model (bayesglm) | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Binary Discriminant Analysis (binda) | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Boosted Tree (blackboost) | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| The Bayesian lasso (blasso) | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bayesian Ridge Regression (Model Averaged) (blassoAveraged) | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bayesian Ridge Regression (bridge) | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bayesian Regularized Neural Networks (brnn) | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Boosted Linear Model (BstLm) | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Boosted Smoothing Spline (bstSm) | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Boosted Tree (bstTree) | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| C5.0 (C5.0) | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| Cost-Sensitive C5.0 (C5.0Cost) | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| Single C5.0 Ruleset (C5.0Rules) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Single C5.0 Tree (C5.0Tree) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Conditional Inference Random Forest (cforest) | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| CHi-squared Automated Interaction Detection (chaid) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| SIMCA (CSimca) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Conditional Inference Tree (ctree) | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Conditional Inference Tree (ctree2) | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Cubist (cubist) | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Diagonal Discriminant Analysis (dda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| DeepBoost (deepboost) | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| Dynamic Evolving Neural-Fuzzy Inference System (DENFIS) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Stacked AutoEncoder Deep Neural Network (dnn) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Linear Distance Weighted Discrimination (dwdLinear) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Distance Weighted Discrimination with Polynomial Kernel (dwdPoly) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Distance Weighted Discrimination with Radial Basis Function Kernel (dwdRadial) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Multivariate Adaptive Regression Spline (earth) | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Extreme Learning Machine (elm) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Elasticnet (enet) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Tree Models from Genetic Algorithms (evtree) | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Random Forest by Randomization (extraTrees) | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Flexible Discriminant Analysis (fda) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Fuzzy Rules Using Genetic Cooperative-Competitive Learning and Pittsburgh (FH.GBML) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Fuzzy Inference Rules by Descent Method (FIR.DM) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Ridge Regression with Variable Selection (foba) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Fuzzy Rules Using Chi’s Method (FRBCS.CHI) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Fuzzy Rules with Weight Factor (FRBCS.W) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Simplified TSK Fuzzy Rules (FS.HGD) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Generalized Additive Model using Splines (gam) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Boosted Generalized Additive Model (gamboost) | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Generalized Additive Model using LOESS (gamLoess) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Generalized Additive Model using Splines (gamSpline) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Gaussian Process (gaussprLinear) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Gaussian Process with Polynomial Kernel (gaussprPoly) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Gaussian Process with Radial Basis Function Kernel (gaussprRadial) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Gradient Boosting Machines (gbm_h2o) | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Stochastic Gradient Boosting (gbm) | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Multivariate Adaptive Regression Splines (gcvEarth) | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Fuzzy Rules via MOGUL (GFS.FR.MOGUL) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Genetic Lateral Tuning and Rule Selection of Linguistic Fuzzy Systems (GFS.LT.RS) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Fuzzy Rules via Thrift (GFS.THRIFT) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Negative Binomial Generalized Linear Model (glm.nb) | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Generalized Linear Model (glm) | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Boosted Generalized Linear Model (glmboost) | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| glmnet (glmnet_h2o) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| glmnet (glmnet) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Generalized Linear Model with Stepwise Feature Selection (glmStepAIC) | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Generalized Partial Least Squares (gpls) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Heteroscedastic Discriminant Analysis (hda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| High Dimensional Discriminant Analysis (hdda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| High-Dimensional Regularized Discriminant Analysis (hdrda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Hybrid Neural Fuzzy Inference System (HYFIS) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Independent Component Regression (icr) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| C4.5-like Trees (J48) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Rule-Based Classifier (JRip) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Partial Least Squares (kernelpls) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| k-Nearest Neighbors (kknn) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| k-Nearest Neighbors (knn) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Polynomial Kernel Regularized Least Squares (krlsPoly) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Radial Basis Function Kernel Regularized Least Squares (krlsRadial) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Least Angle Regression (lars) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Least Angle Regression (lars2) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| The lasso (lasso) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Linear Discriminant Analysis (lda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Linear Discriminant Analysis (lda2) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Linear Regression with Backwards Selection (leapBackward) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Linear Regression with Forward Selection (leapForward) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Linear Regression with Stepwise Selection (leapSeq) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Robust Linear Discriminant Analysis (Linda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Linear Regression (lm) | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Linear Regression with Stepwise Selection (lmStepAIC) | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Logistic Model Trees (LMT) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Localized Linear Discriminant Analysis (loclda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bagged Logic Regression (logicBag) | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Boosted Logistic Regression (LogitBoost) | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Logic Regression (logreg) | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Least Squares Support Vector Machine (lssvmLinear) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Least Squares Support Vector Machine with Polynomial Kernel (lssvmPoly) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Least Squares Support Vector Machine with Radial Basis Function Kernel (lssvmRadial) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Learning Vector Quantization (lvq) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Model Tree (M5) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| Model Rules (M5Rules) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Model Averaged Naive Bayes Classifier (manb) | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Mixture Discriminant Analysis (mda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Maximum Uncertainty Linear Discriminant Analysis (Mlda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Multi-Layer Perceptron (mlp) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Multilayer Perceptron Network with Weight Decay (mlpKerasDecay) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Multilayer Perceptron Network with Weight Decay (mlpKerasDecayCost) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Multilayer Perceptron Network with Dropout (mlpKerasDropout) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Multilayer Perceptron Network with Dropout (mlpKerasDropoutCost) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Multi-Layer Perceptron, with multiple layers (mlpML) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Multilayer Perceptron Network by Stochastic Gradient Descent (mlpSGD) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Multi-Layer Perceptron (mlpWeightDecay) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Multi-Layer Perceptron, multiple layers (mlpWeightDecayML) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Monotone Multi-Layer Perceptron Neural Network (monmlp) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Multi-Step Adaptive MCP-Net (msaenet) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Penalized Multinomial Regression (multinom) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Neural Network (mxnet) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Neural Network (mxnetAdam) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Naive Bayes (naive_bayes) | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Naive Bayes (nb) | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Naive Bayes Classifier (nbDiscrete) | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Semi-Naive Structure Learner Wrapper (nbSearch) | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Neural Network (neuralnet) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Neural Network (nnet) | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Non-Negative Least Squares (nnls) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Tree-Based Ensembles (nodeHarvest) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| Non-Informative Model (null) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Single Rule Classification (OneR) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Penalized Ordinal Regression (ordinalNet) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Oblique Random Forest (ORFlog) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Oblique Random Forest (ORFpls) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Oblique Random Forest (ORFridge) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Oblique Random Forest (ORFsvm) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Optimal Weighted Nearest Neighbor Classifier (ownn) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Nearest Shrunken Centroids (pam) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Parallel Random Forest (parRF) | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Rule-Based Classifier (PART) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| partDSA (partDSA) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Neural Networks with Feature Extraction (pcaNNet) | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Principal Component Analysis (pcr) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Penalized Discriminant Analysis (pda) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Penalized Discriminant Analysis (pda2) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Penalized Linear Regression (penalized) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Penalized Linear Discriminant Analysis (PenalizedLDA) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Penalized Logistic Regression (plr) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Partial Least Squares (pls) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Partial Least Squares Generalized Linear Models (plsRglm) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Ordered Logistic or Probit Regression (polr) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Projection Pursuit Regression (ppr) | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Patient Rule Induction Method (PRIM) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Greedy Prototype Selection (protoclass) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Quadratic Discriminant Analysis (qda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Robust Quadratic Discriminant Analysis (QdaCov) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Quantile Random Forest (qrf) | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Quantile Regression Neural Network (qrnn) | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Ensembles of Generalized Linear Models (randomGLM) | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Random Forest (ranger) | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Radial Basis Function Network (rbf) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Radial Basis Function Network (rbfDDA) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Random Forest (Rborist) | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Regularized Discriminant Analysis (rda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Regularized Logistic Regression (regLogistic) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Relaxed Lasso (relaxo) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Random Forest (rf) | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Random Ferns (rFerns) | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Factor-Based Linear Discriminant Analysis (RFlda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Random Forest Rule-Based Model (rfRules) | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Ridge Regression (ridge) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Regularized Linear Discriminant Analysis (rlda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Robust Linear Model (rlm) | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Robust Mixture Discriminant Analysis (rmda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ROC-Based Classifier (rocc) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Rotation Forest (rotationForest) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| Rotation Forest (rotationForestCp) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| CART (rpart) | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| CART (rpart1SE) | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| CART (rpart2) | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Cost-Sensitive CART (rpartCost) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| CART or Ordinal Responses (rpartScore) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Quantile Regression with LASSO penalty (rqlasso) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Non-Convex Penalized Quantile Regression (rqnc) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Regularized Random Forest (RRF) | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Regularized Random Forest (RRFglobal) | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Robust Regularized Linear Discriminant Analysis (rrlda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Robust SIMCA (RSimca) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Relevance Vector Machines with Linear Kernel (rvmLinear) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Relevance Vector Machines with Polynomial Kernel (rvmPoly) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Relevance Vector Machines with Radial Basis Function Kernel (rvmRadial) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Subtractive Clustering and Fuzzy c-Means Rules (SBC) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Shrinkage Discriminant Analysis (sda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sparse Distance Weighted Discrimination (sdwd) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Partial Least Squares (simpls) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Fuzzy Rules Using the Structural Learning Algorithm on Vague Environment (SLAVE) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Stabilized Linear Discriminant Analysis (slda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sparse Mixture Discriminant Analysis (smda) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Stabilized Nearest Neighbor Classifier (snn) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sparse Linear Discriminant Analysis (sparseLDA) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Spike and Slab Regression (spikeslab) | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sparse Partial Least Squares (spls) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Linear Discriminant Analysis with Stepwise Feature Selection (stepLDA) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Quadratic Discriminant Analysis with Stepwise Feature Selection (stepQDA) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Supervised Principal Component Analysis (superpc) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Support Vector Machines with Boundrange String Kernel (svmBoundrangeString) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| Support Vector Machines with Exponential String Kernel (svmExpoString) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| Support Vector Machines with Linear Kernel (svmLinear) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Support Vector Machines with Linear Kernel (svmLinear2) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| L2 Regularized Support Vector Machine (dual) with Linear Kernel (svmLinear3) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Linear Support Vector Machines with Class Weights (svmLinearWeights) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| L2 Regularized Linear Support Vector Machines with Class Weights (svmLinearWeights2) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| Support Vector Machines with Polynomial Kernel (svmPoly) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Support Vector Machines with Radial Basis Function Kernel (svmRadial) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Support Vector Machines with Radial Basis Function Kernel (svmRadialCost) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Support Vector Machines with Radial Basis Function Kernel (svmRadialSigma) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Support Vector Machines with Class Weights (svmRadialWeights) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| Support Vector Machines with Spectrum String Kernel (svmSpectrumString) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| Tree Augmented Naive Bayes Classifier (tan) | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Tree Augmented Naive Bayes Classifier Structure Learner Wrapper (tanSearch) | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bagged CART (treebag) | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Variational Bayesian Multinomial Probit Regression (vbmpRadial) | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Adjacent Categories Probability Model for Ordinal Data (vglmAdjCat) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Continuation Ratio Model for Ordinal Data (vglmContRatio) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Cumulative Probability Model for Ordinal Data (vglmCumulative) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Partial Least Squares (widekernelpls) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Wang and Mendel Fuzzy Rules (WM) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Weighted Subspace Random Forest (wsrf) | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| eXtreme Gradient Boosting (xgbDART) | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| eXtreme Gradient Boosting (xgbLinear) | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| eXtreme Gradient Boosting (xgbTree) | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Self-Organizing Maps (xyf) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
- Pueden ver base de datos acá
Probemos una vez con train y rpart (regression trees)
Class <- train(Species ~ ., data = Train, method = "rpart", trControl = fitControl) postResample(pred = predict(Class, Train), obs = Train$Species)
## Accuracy Kappa ## 0.96 0.94
postResample(pred = predict(Class, Test), obs = Test$Species)
## Accuracy Kappa ## 0.9466667 0.9200000
¿Que es Accuracy?
- Muchas medidas acá
\[Accuracy = \frac{Correctos}{Totales}\]
confusionMatrix(data = predict(Class, Test), reference = Test$Species)
## Confusion Matrix and Statistics ## ## Reference ## Prediction setosa versicolor virginica ## setosa 25 0 0 ## versicolor 0 23 2 ## virginica 0 2 23 ## ## Overall Statistics ## ## Accuracy : 0.9467 ## 95% CI : (0.869, 0.9853) ## No Information Rate : 0.3333 ## P-Value [Acc > NIR] : < 2.2e-16 ## ## Kappa : 0.92 ## ## Mcnemar's Test P-Value : NA ## ## Statistics by Class: ## ## Class: setosa Class: versicolor Class: virginica ## Sensitivity 1.0000 0.9200 0.9200 ## Specificity 1.0000 0.9600 0.9600 ## Pos Pred Value 1.0000 0.9200 0.9200 ## Neg Pred Value 1.0000 0.9600 0.9600 ## Prevalence 0.3333 0.3333 0.3333 ## Detection Rate 0.3333 0.3067 0.3067 ## Detection Prevalence 0.3333 0.3333 0.3333 ## Balanced Accuracy 1.0000 0.9400 0.9400
¿Que nos dice este modelo?
¿Que variables explican?
plot(varImp(Class))
Caracteres buenos para clasificar
Caracteres malos para clasificar
Como mejorar o empeorar un modelo
- Parametros
plot(Class)
Que es CP?
| cp | Accuracy | Kappa | AccuracySD | KappaSD |
|---|---|---|---|---|
| 0.00 | 0.925 | 0.886 | 0.102 | 0.156 |
| 0.44 | 0.707 | 0.572 | 0.130 | 0.182 |
| 0.50 | 0.366 | 0.116 | 0.135 | 0.182 |
- Complexity parameter
¿Como lo controlo?
rpartGrid <- expand.grid(cp = c(0.48, 0.8, 1))
Class2 <- train(Species ~ ., data = Train, method = "rpart", trControl = fitControl,
tuneGrid = rpartGrid)
plot(Class2)
¿Que tan malo es esto?
postResample(pred = predict(Class2, Train), obs = Train$Species)
## Accuracy Kappa ## 0.6666667 0.5000000
postResample(pred = predict(Class2, Test), obs = Test$Species)
## Accuracy Kappa ## 0.6666667 0.5000000
A ver?
rpart.plot.version1(Class2$finalModel)
¿Como lo controlo?
rpartGrid <- expand.grid(cp = seq(0.01, 1, by = 0.01))
Class3 <- train(Species ~ ., data = Train, method = "rpart", trControl = fitControl,
tuneGrid = rpartGrid)
plot(Class3)
¿Que tan bueno es esto?
postResample(pred = predict(Class3, Train), obs = Train$Species)
## Accuracy Kappa ## 0.96 0.94
postResample(pred = predict(Class3, Test), obs = Test$Species)
## Accuracy Kappa ## 0.9466667 0.9200000
A ver?
rpart.plot(Class3$finalModel)
¿De donde saco los parámetros de cada algorítmo?
De la página de caret
Ahora regresión
Donde vive el guanaco?
Bajar bases de datos
- Base de datos sp2.rds y SA.rds
githubURL <- ("https://raw.githubusercontent.com/derek-corcoran-barrios/derek-corcoran-barrios.github.io/master/CursoMultiPres/Capitulo_6/SA.rds")
download.file(githubURL, "SA.rds", method = "curl")
SA <- readRDS("SA.rds")
githubURL <- ("https://raw.githubusercontent.com/derek-corcoran-barrios/derek-corcoran-barrios.github.io/master/CursoMultiPres/Capitulo_6/sp2.rds")
download.file(githubURL, "sp2.rds", method = "curl")
sp2 <- read_rds("sp2.rds")
githubURL <- ("https://raw.githubusercontent.com/derek-corcoran-barrios/derek-corcoran-barrios.github.io/master/CursoMultiPres/Capitulo_6/sp.rds")
download.file(githubURL, "sp.rds", method = "curl")
sp <- read_rds("sp.rds")
Veamos
¿Que variables tenemos?
| presence | TempMedia | TempMesCalido | TempMesFrio | TempRangoAnual | PPAnual | PPMesSeco | PPMesHum |
|---|---|---|---|---|---|---|---|
| 1 | 16.4 | 26.0 | 7.6 | 18.4 | 37 | 12 | 0 |
| 1 | 15.2 | 25.1 | 5.8 | 19.3 | 31 | 10 | 0 |
| 1 | 19.8 | 28.0 | 11.8 | 16.2 | 17 | 4 | 0 |
| 1 | 17.4 | 26.7 | 9.1 | 17.6 | 38 | 12 | 0 |
| 1 | 1.5 | 10.0 | -5.7 | 15.7 | 1474 | 144 | 101 |
| 1 | 15.0 | 23.8 | 7.1 | 16.7 | 66 | 18 | 0 |
| 1 | 7.7 | 17.4 | -0.8 | 18.2 | 696 | 91 | 32 |
| 1 | 6.9 | 16.8 | -2.0 | 18.8 | 578 | 73 | 27 |
| 1 | 7.7 | 17.4 | -0.8 | 18.2 | 696 | 91 | 32 |
| 1 | 1.5 | 10.0 | -5.7 | 15.7 | 1474 | 144 | 101 |
| 1 | 7.7 | 17.4 | -0.8 | 18.2 | 696 | 91 | 32 |
| 1 | 7.1 | 16.9 | -1.7 | 18.6 | 604 | 77 | 28 |
| 1 | 7.3 | 17.4 | -1.7 | 19.1 | 495 | 64 | 22 |
| 1 | 5.7 | 15.8 | -2.9 | 18.7 | 791 | 87 | 49 |
| 1 | 8.1 | 22.0 | -1.8 | 23.8 | 783 | 137 | 22 |
| 1 | 8.2 | 22.2 | -1.7 | 23.9 | 760 | 139 | 21 |
| 1 | 5.0 | 13.0 | -1.8 | 14.8 | 677 | 66 | 42 |
| 1 | 5.7 | 15.8 | -2.9 | 18.7 | 791 | 87 | 49 |
| 1 | 5.7 | 15.8 | -2.9 | 18.7 | 791 | 87 | 49 |
| 1 | 5.7 | 15.8 | -2.9 | 18.7 | 791 | 87 | 49 |
| 1 | 5.7 | 15.8 | -2.9 | 18.7 | 791 | 87 | 49 |
| 1 | 7.8 | 18.0 | -0.8 | 18.8 | 778 | 86 | 46 |
| 1 | 5.7 | 15.8 | -2.9 | 18.7 | 791 | 87 | 49 |
| 1 | 8.2 | 22.1 | -1.7 | 23.8 | 804 | 142 | 22 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 8.2 | 22.1 | -1.7 | 23.8 | 804 | 142 | 22 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 5.0 | 13.0 | -1.8 | 14.8 | 677 | 66 | 42 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 8.1 | 22.0 | -1.8 | 23.8 | 783 | 137 | 22 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 7.5 | 17.8 | -1.1 | 18.9 | 766 | 88 | 43 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 8.2 | 22.1 | -1.7 | 23.8 | 804 | 142 | 22 |
| 1 | 5.8 | 19.4 | -3.7 | 23.1 | 800 | 146 | 20 |
| 1 | 5.0 | 13.0 | -1.8 | 14.8 | 677 | 66 | 42 |
| 1 | 6.6 | 16.1 | -1.0 | 17.1 | 455 | 45 | 32 |
| 1 | 6.5 | 16.4 | -2.3 | 18.7 | 663 | 69 | 43 |
| 1 | 6.2 | 16.2 | -2.9 | 19.1 | 559 | 59 | 35 |
| 1 | 5.4 | 16.2 | -4.4 | 20.6 | 315 | 43 | 16 |
| 1 | 4.8 | 12.7 | -2.0 | 14.7 | 674 | 66 | 42 |
| 1 | 3.5 | 14.0 | -6.0 | 20.0 | 406 | 52 | 21 |
| 1 | 5.0 | 15.5 | -4.5 | 20.0 | 389 | 48 | 21 |
| 1 | 5.1 | 15.6 | -4.5 | 20.1 | 369 | 47 | 19 |
| 1 | 5.1 | 15.6 | -4.5 | 20.1 | 369 | 47 | 19 |
| 1 | 3.4 | 11.5 | -3.4 | 14.9 | 685 | 69 | 43 |
| 1 | 5.4 | 16.1 | -4.3 | 20.4 | 329 | 44 | 17 |
| 1 | 3.4 | 11.5 | -3.4 | 14.9 | 685 | 69 | 43 |
| 1 | 5.1 | 15.6 | -4.5 | 20.1 | 369 | 47 | 19 |
| 1 | 5.1 | 15.6 | -4.5 | 20.1 | 369 | 47 | 19 |
| 1 | 6.0 | 16.2 | -3.1 | 19.3 | 559 | 61 | 34 |
| 1 | 7.4 | 17.5 | -1.7 | 19.2 | 533 | 58 | 32 |
| 1 | 5.1 | 15.6 | -4.5 | 20.1 | 369 | 47 | 19 |
| 1 | 6.3 | 16.3 | -2.6 | 18.9 | 670 | 71 | 43 |
| 1 | 5.1 | 15.6 | -4.5 | 20.1 | 369 | 47 | 19 |
| 1 | 6.9 | 16.9 | -2.2 | 19.1 | 575 | 62 | 35 |
| 1 | 6.9 | 16.9 | -2.2 | 19.1 | 575 | 62 | 35 |
| 1 | 5.7 | 15.8 | -2.9 | 18.7 | 791 | 87 | 49 |
| 1 | 7.9 | 18.1 | -0.7 | 18.8 | 738 | 83 | 43 |
| 1 | 5.7 | 15.8 | -2.9 | 18.7 | 791 | 87 | 49 |
| 1 | 5.7 | 15.8 | -2.9 | 18.7 | 791 | 87 | 49 |
| 1 | 5.1 | 15.6 | -4.5 | 20.1 | 369 | 47 | 19 |
| 1 | 2.5 | 11.0 | -4.5 | 15.5 | 549 | 55 | 33 |
| 1 | 3.0 | 11.2 | -3.8 | 15.0 | 623 | 63 | 38 |
| 1 | 10.5 | 23.1 | 0.1 | 23.0 | 217 | 27 | 13 |
| 1 | 10.6 | 23.3 | 0.0 | 23.3 | 221 | 28 | 13 |
| 1 | 5.0 | 13.0 | -1.8 | 14.8 | 677 | 66 | 42 |
| 1 | 5.1 | 15.6 | -4.5 | 20.1 | 369 | 47 | 19 |
| 1 | 10.5 | 23.2 | -0.1 | 23.3 | 222 | 28 | 13 |
| 1 | 5.1 | 15.6 | -4.5 | 20.1 | 369 | 47 | 19 |
| 1 | 3.4 | 11.5 | -3.4 | 14.9 | 685 | 69 | 43 |
| 1 | 5.1 | 15.6 | -4.5 | 20.1 | 369 | 47 | 19 |
| 1 | 5.4 | 16.1 | -4.2 | 20.3 | 345 | 45 | 18 |
| 1 | 6.2 | 16.4 | -2.2 | 18.6 | 808 | 91 | 48 |
| 1 | 7.9 | 18.2 | -0.7 | 18.9 | 727 | 83 | 41 |
| 1 | 7.9 | 18.2 | -0.7 | 18.9 | 727 | 83 | 41 |
| 1 | 6.4 | 16.7 | -2.2 | 18.9 | 735 | 84 | 43 |
| 1 | 0.5 | 10.8 | -8.8 | 19.6 | 541 | 60 | 25 |
| 1 | 6.3 | 16.3 | -2.6 | 18.9 | 670 | 71 | 43 |
| 1 | 6.2 | 16.4 | -2.2 | 18.6 | 808 | 91 | 48 |
| 1 | 7.5 | 17.8 | -1.1 | 18.9 | 766 | 88 | 43 |
| 1 | 7.3 | 17.5 | -1.9 | 19.4 | 496 | 54 | 29 |
| 1 | 3.5 | 11.6 | -3.2 | 14.8 | 668 | 68 | 41 |
| 1 | 6.9 | 16.9 | -2.2 | 19.1 | 575 | 62 | 35 |
| 1 | 7.0 | 17.2 | -2.3 | 19.5 | 466 | 51 | 27 |
| 1 | 7.5 | 17.8 | -1.1 | 18.9 | 766 | 88 | 43 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 6.3 | 16.3 | -2.6 | 18.9 | 670 | 71 | 43 |
| 1 | 7.0 | 17.2 | -2.3 | 19.5 | 466 | 51 | 27 |
| 1 | 7.3 | 17.5 | -1.9 | 19.4 | 496 | 54 | 29 |
| 1 | 5.1 | 15.6 | -4.5 | 20.1 | 369 | 47 | 19 |
| 1 | 10.4 | 23.2 | -0.2 | 23.4 | 221 | 28 | 12 |
| 1 | 7.3 | 17.5 | -1.9 | 19.4 | 496 | 54 | 29 |
| 1 | 7.5 | 17.8 | -1.1 | 18.9 | 766 | 88 | 43 |
| 1 | 7.5 | 17.8 | -1.1 | 18.9 | 766 | 88 | 43 |
| 1 | 7.4 | 17.5 | -1.7 | 19.2 | 533 | 58 | 32 |
| 1 | 10.6 | 23.3 | 0.0 | 23.3 | 221 | 28 | 13 |
| 1 | 6.3 | 16.3 | -2.6 | 18.9 | 670 | 71 | 43 |
| 1 | 3.4 | 11.5 | -3.4 | 14.9 | 685 | 69 | 43 |
| 1 | 5.2 | 15.8 | -4.4 | 20.2 | 351 | 46 | 18 |
| 1 | 4.2 | 12.7 | -2.7 | 15.4 | 501 | 50 | 29 |
| 1 | 1.5 | 12.1 | -8.1 | 20.2 | 442 | 57 | 22 |
| 1 | 3.2 | 11.2 | -3.7 | 14.9 | 681 | 68 | 42 |
| 1 | 5.5 | 16.1 | -4.0 | 20.1 | 364 | 45 | 20 |
| 1 | 4.6 | 12.8 | -2.3 | 15.1 | 554 | 54 | 34 |
| 1 | 5.2 | 15.9 | -4.4 | 20.3 | 331 | 44 | 17 |
| 1 | 5.3 | 13.7 | -1.8 | 15.5 | 495 | 48 | 30 |
| 1 | 5.3 | 13.4 | -1.6 | 15.0 | 559 | 54 | 34 |
| 1 | 11.2 | 23.8 | 0.6 | 23.2 | 220 | 28 | 13 |
| 1 | 10.4 | 23.0 | 0.0 | 23.0 | 216 | 27 | 12 |
| 1 | 11.0 | 23.5 | 0.6 | 22.9 | 221 | 28 | 13 |
| 1 | 5.1 | 14.2 | -2.2 | 16.4 | 382 | 40 | 21 |
| 1 | 5.1 | 14.2 | -2.2 | 16.4 | 382 | 40 | 21 |
| 1 | 1.0 | 11.4 | -8.5 | 19.9 | 495 | 56 | 22 |
| 1 | 5.1 | 14.2 | -2.2 | 16.4 | 382 | 40 | 21 |
| 1 | 5.0 | 15.5 | -4.5 | 20.0 | 389 | 48 | 21 |
| 1 | 10.0 | 20.9 | -2.9 | 23.8 | 162 | 75 | 0 |
| 1 | 10.5 | 23.1 | 0.1 | 23.0 | 217 | 27 | 13 |
| 1 | 3.5 | 14.0 | -6.0 | 20.0 | 406 | 52 | 21 |
| 1 | 5.0 | 15.5 | -4.5 | 20.0 | 389 | 48 | 21 |
| 1 | 5.0 | 15.5 | -4.5 | 20.0 | 389 | 48 | 21 |
| 1 | 5.3 | 16.0 | -4.3 | 20.3 | 346 | 45 | 18 |
| 1 | 5.0 | 13.0 | -1.8 | 14.8 | 677 | 66 | 42 |
| 1 | 4.9 | 14.8 | -4.0 | 18.8 | 676 | 72 | 44 |
| 1 | 5.3 | 16.0 | -4.3 | 20.3 | 346 | 45 | 18 |
| 1 | 5.3 | 16.0 | -4.3 | 20.3 | 346 | 45 | 18 |
| 1 | 10.5 | 23.2 | -0.1 | 23.3 | 223 | 28 | 13 |
| 1 | 6.2 | 16.4 | -2.2 | 18.6 | 808 | 91 | 48 |
| 1 | 8.2 | 22.2 | -1.7 | 23.9 | 760 | 139 | 21 |
| 1 | 7.9 | 18.2 | -0.8 | 19.0 | 690 | 80 | 38 |
| 1 | 7.9 | 18.2 | -0.8 | 19.0 | 690 | 80 | 38 |
| 1 | 7.9 | 18.2 | -0.8 | 19.0 | 690 | 80 | 38 |
| 1 | 7.9 | 18.2 | -0.7 | 18.9 | 727 | 83 | 41 |
| 1 | 7.9 | 18.2 | -0.7 | 18.9 | 727 | 83 | 41 |
| 1 | 7.9 | 18.2 | -0.8 | 19.0 | 690 | 80 | 38 |
| 1 | 7.9 | 18.2 | -0.8 | 19.0 | 690 | 80 | 38 |
| 1 | 7.9 | 18.2 | -0.8 | 19.0 | 690 | 80 | 38 |
| 1 | 7.9 | 18.2 | -0.8 | 19.0 | 690 | 80 | 38 |
| 1 | 7.9 | 18.2 | -0.8 | 19.0 | 690 | 80 | 38 |
| 1 | 7.9 | 18.2 | -0.8 | 19.0 | 690 | 80 | 38 |
| 1 | 15.3 | 25.0 | 6.0 | 19.0 | 31 | 10 | 0 |
| 1 | 7.9 | 18.2 | -0.8 | 19.0 | 690 | 80 | 38 |
| 1 | 16.6 | 26.0 | 8.0 | 18.0 | 38 | 12 | 0 |
| 1 | 16.6 | 26.0 | 8.0 | 18.0 | 38 | 12 | 0 |
| 1 | 7.9 | 18.2 | -0.8 | 19.0 | 690 | 80 | 38 |
| 1 | 6.2 | 16.4 | -2.2 | 18.6 | 808 | 91 | 48 |
| 1 | 7.9 | 18.2 | -0.7 | 18.9 | 727 | 83 | 41 |
| 1 | 8.2 | 23.0 | -3.2 | 26.2 | 904 | 201 | 7 |
| 1 | 8.2 | 23.0 | -3.2 | 26.2 | 904 | 201 | 7 |
| 0 | 22.3 | 31.6 | 11.9 | 19.7 | 1424 | 198 | 50 |
| 0 | 22.3 | 30.2 | 12.7 | 17.5 | 1643 | 270 | 19 |
| 0 | 25.6 | 31.0 | 20.3 | 10.7 | 3096 | 322 | 178 |
| 0 | 24.7 | 31.1 | 18.6 | 12.5 | 1822 | 317 | 39 |
| 0 | 26.1 | 32.9 | 18.9 | 14.0 | 2088 | 271 | 74 |
| 0 | 19.4 | 27.8 | 11.0 | 16.8 | 1463 | 172 | 84 |
| 0 | 19.0 | 28.9 | 10.0 | 18.9 | 1528 | 149 | 109 |
| 0 | 11.9 | 18.4 | 6.0 | 12.4 | 1392 | 163 | 71 |
| 0 | 15.9 | 31.7 | 2.5 | 29.2 | 792 | 101 | 27 |
| 0 | 25.3 | 31.0 | 20.2 | 10.8 | 3891 | 428 | 194 |
| 0 | 27.3 | 34.3 | 22.1 | 12.2 | 2915 | 435 | 59 |
| 0 | 24.6 | 30.9 | 19.8 | 11.1 | 1748 | 278 | 36 |
| 0 | 22.4 | 29.2 | 14.7 | 14.5 | 1385 | 176 | 61 |
| 0 | 25.5 | 32.4 | 20.1 | 12.3 | 2842 | 427 | 49 |
| 0 | 9.7 | 25.6 | -2.8 | 28.4 | 207 | 32 | 10 |
| 0 | 25.9 | 31.9 | 20.8 | 11.1 | 3157 | 372 | 131 |
| 0 | 24.9 | 35.6 | 13.5 | 22.1 | 2280 | 386 | 5 |
| 0 | 26.1 | 32.9 | 20.1 | 12.8 | 1728 | 249 | 23 |
| 0 | 26.0 | 31.8 | 20.5 | 11.3 | 2068 | 197 | 121 |
| 0 | 27.1 | 33.4 | 22.1 | 11.3 | 2325 | 391 | 93 |
| 0 | 22.0 | 34.4 | 11.1 | 23.3 | 1479 | 164 | 69 |
| 0 | 24.9 | 32.1 | 19.9 | 12.2 | 2088 | 372 | 43 |
| 0 | 26.9 | 33.0 | 21.2 | 11.8 | 2264 | 312 | 76 |
| 0 | 27.9 | 35.8 | 22.2 | 13.6 | 2084 | 369 | 5 |
| 0 | 25.0 | 34.6 | 14.1 | 20.5 | 845 | 125 | 15 |
| 0 | 24.8 | 33.1 | 16.8 | 16.3 | 1231 | 193 | 3 |
| 0 | 26.0 | 33.7 | 20.8 | 12.9 | 2141 | 393 | 65 |
| 0 | 7.5 | 18.5 | -6.5 | 25.0 | 428 | 111 | 2 |
| 0 | 4.0 | 13.3 | -5.2 | 18.5 | 78 | 12 | 3 |
| 0 | 25.2 | 33.1 | 15.2 | 17.9 | 1766 | 281 | 7 |
| 0 | 6.5 | 15.8 | -1.0 | 16.8 | 262 | 32 | 13 |
| 0 | 26.3 | 34.1 | 18.5 | 15.6 | 1540 | 291 | 3 |
| 0 | 26.4 | 34.8 | 17.9 | 16.9 | 1859 | 293 | 6 |
| 0 | 24.4 | 32.6 | 14.0 | 18.6 | 1530 | 268 | 12 |
| 0 | 22.1 | 35.5 | 8.1 | 27.4 | 656 | 113 | 8 |
| 0 | 22.2 | 31.0 | 11.7 | 19.3 | 1040 | 219 | 3 |
| 0 | 9.2 | 21.4 | -2.2 | 23.6 | 166 | 21 | 9 |
| 0 | 22.1 | 27.9 | 16.2 | 11.7 | 2525 | 404 | 49 |
| 0 | 17.5 | 31.4 | 2.5 | 28.9 | 468 | 102 | 7 |
| 0 | 26.3 | 32.0 | 20.8 | 11.2 | 2677 | 345 | 84 |
| 0 | 14.3 | 31.7 | -1.1 | 32.8 | 266 | 37 | 8 |
| 0 | 19.7 | 32.4 | 8.4 | 24.0 | 1080 | 148 | 43 |
| 0 | 19.9 | 33.6 | 7.1 | 26.5 | 985 | 141 | 27 |
| 0 | 28.3 | 35.8 | 22.7 | 13.1 | 2535 | 403 | 29 |
| 0 | 26.8 | 34.4 | 21.4 | 13.0 | 2174 | 315 | 7 |
| 0 | 20.9 | 30.7 | 10.3 | 20.4 | 1460 | 162 | 74 |
| 0 | 24.8 | 31.4 | 17.0 | 14.4 | 2867 | 393 | 91 |
| 0 | 27.2 | 35.9 | 19.6 | 16.3 | 1421 | 337 | 7 |
| 0 | 19.9 | 28.7 | 10.3 | 18.4 | 1591 | 209 | 80 |
| 0 | 2.8 | 10.3 | -7.7 | 18.0 | 604 | 150 | 2 |
| 0 | 26.5 | 33.8 | 21.4 | 12.4 | 2261 | 370 | 86 |
| 0 | 26.4 | 32.7 | 21.1 | 11.6 | 1793 | 320 | 59 |
| 0 | 21.9 | 35.3 | 8.0 | 27.3 | 605 | 114 | 6 |
| 0 | 26.1 | 33.7 | 18.5 | 15.2 | 605 | 151 | 0 |
| 0 | 16.1 | 32.3 | 0.1 | 32.2 | 225 | 39 | 5 |
| 0 | 22.5 | 30.2 | 13.1 | 17.1 | 1600 | 274 | 24 |
| 0 | 27.7 | 35.1 | 22.0 | 13.1 | 1599 | 318 | 3 |
| 0 | 27.2 | 32.7 | 22.7 | 10.0 | 1456 | 207 | 46 |
| 0 | 25.1 | 33.6 | 16.6 | 17.0 | 1282 | 227 | 1 |
| 0 | 27.7 | 35.6 | 21.3 | 14.3 | 1478 | 249 | 7 |
| 0 | 19.0 | 30.5 | 5.0 | 25.5 | 780 | 168 | 4 |
| 0 | 25.6 | 30.9 | 20.0 | 10.9 | 2784 | 313 | 152 |
| 0 | 19.6 | 29.9 | 10.6 | 19.3 | 1327 | 147 | 79 |
| 0 | 20.8 | 34.7 | 5.6 | 29.1 | 403 | 79 | 4 |
| 0 | 26.2 | 34.4 | 15.6 | 18.8 | 1342 | 248 | 17 |
| 0 | 26.5 | 31.7 | 21.6 | 10.1 | 1728 | 252 | 73 |
| 0 | 20.3 | 32.3 | 6.2 | 26.1 | 717 | 151 | 2 |
| 0 | 23.1 | 29.5 | 17.0 | 12.5 | 1023 | 142 | 49 |
| 0 | 24.1 | 31.1 | 16.8 | 14.3 | 973 | 161 | 39 |
| 0 | 20.6 | 33.1 | 9.1 | 24.0 | 1119 | 144 | 35 |
| 0 | 14.5 | 23.3 | 4.2 | 19.1 | 44 | 19 | 0 |
| 0 | 18.6 | 26.4 | 12.2 | 14.2 | 6 | 1 | 0 |
| 0 | 26.7 | 32.5 | 21.6 | 10.9 | 2198 | 354 | 85 |
| 0 | 13.0 | 18.8 | 7.7 | 11.1 | 607 | 91 | 18 |
| 0 | 22.3 | 30.9 | 11.4 | 19.5 | 1201 | 159 | 36 |
| 0 | 26.2 | 33.5 | 18.7 | 14.8 | 2171 | 310 | 31 |
| 0 | 23.5 | 31.0 | 14.0 | 17.0 | 1593 | 289 | 18 |
| 0 | 25.3 | 33.6 | 16.8 | 16.8 | 2274 | 371 | 11 |
| 0 | 24.3 | 32.2 | 14.2 | 18.0 | 1444 | 275 | 20 |
| 0 | 18.3 | 32.9 | 3.7 | 29.2 | 451 | 92 | 6 |
| 0 | 15.2 | 32.7 | 0.9 | 31.8 | 397 | 55 | 15 |
| 0 | 18.8 | 31.7 | 4.3 | 27.4 | 685 | 130 | 16 |
| 0 | 26.0 | 30.9 | 21.4 | 9.5 | 7504 | 824 | 493 |
| 0 | 24.3 | 31.9 | 14.7 | 17.2 | 1511 | 270 | 26 |
| 0 | 27.3 | 34.0 | 21.2 | 12.8 | 1621 | 361 | 14 |
| 0 | 4.6 | 9.8 | -0.3 | 10.1 | 771 | 110 | 17 |
| 0 | 26.6 | 32.3 | 21.7 | 10.6 | 2300 | 390 | 27 |
| 0 | 22.3 | 30.1 | 13.8 | 16.3 | 679 | 141 | 3 |
| 0 | 19.4 | 27.5 | 9.7 | 17.8 | 1002 | 193 | 10 |
| 0 | 21.0 | 29.5 | 11.0 | 18.5 | 1257 | 270 | 11 |
| 0 | 7.6 | 22.5 | -3.7 | 26.2 | 288 | 54 | 8 |
| 0 | 26.3 | 31.3 | 21.4 | 9.9 | 2948 | 328 | 180 |
| 0 | 26.4 | 34.4 | 18.7 | 15.7 | 1662 | 274 | 6 |
| 0 | 20.5 | 28.1 | 10.4 | 17.7 | 1526 | 307 | 12 |
| 0 | 19.9 | 32.9 | 4.8 | 28.1 | 723 | 136 | 10 |
| 0 | 25.2 | 33.2 | 15.0 | 18.2 | 1542 | 266 | 35 |
| 0 | 26.5 | 34.2 | 18.6 | 15.6 | 1690 | 265 | 14 |
| 0 | 23.3 | 31.3 | 15.9 | 15.4 | 645 | 94 | 14 |
| 0 | 11.4 | 21.0 | -1.1 | 22.1 | 661 | 131 | 1 |
| 0 | 26.6 | 32.1 | 21.1 | 11.0 | 2223 | 230 | 128 |
| 0 | 12.7 | 21.7 | 1.0 | 20.7 | 662 | 133 | 2 |
| 0 | 26.7 | 32.7 | 21.4 | 11.3 | 2112 | 385 | 72 |
| 0 | 27.0 | 32.4 | 22.2 | 10.2 | 2490 | 435 | 21 |
| 0 | 24.4 | 33.3 | 13.1 | 20.2 | 1355 | 235 | 21 |
| 0 | 9.2 | 22.6 | -1.9 | 24.5 | 227 | 30 | 9 |
| 0 | 2.7 | 12.9 | -6.1 | 19.0 | 701 | 78 | 46 |
| 0 | 26.6 | 34.4 | 18.7 | 15.7 | 1648 | 258 | 14 |
| 0 | 6.4 | 14.9 | -0.7 | 15.6 | 1463 | 145 | 98 |
| 0 | 26.3 | 32.7 | 20.0 | 12.7 | 2532 | 334 | 52 |
| 0 | 26.2 | 34.3 | 16.5 | 17.8 | 1221 | 210 | 22 |
| 0 | 10.1 | 25.7 | -3.9 | 29.6 | 404 | 51 | 23 |
| 0 | 25.5 | 31.6 | 19.7 | 11.9 | 2028 | 307 | 95 |
| 0 | 26.8 | 33.7 | 20.8 | 12.9 | 3437 | 455 | 138 |
| 0 | 22.6 | 29.7 | 16.5 | 13.2 | 2203 | 242 | 144 |
| 0 | 25.9 | 34.1 | 15.7 | 18.4 | 1354 | 227 | 14 |
| 0 | 26.3 | 34.5 | 18.3 | 16.2 | 760 | 167 | 1 |
| 0 | 22.2 | 28.8 | 14.8 | 14.0 | 697 | 121 | 14 |
| 0 | 20.8 | 31.8 | 7.0 | 24.8 | 1090 | 205 | 4 |
| 0 | 25.5 | 31.1 | 20.3 | 10.8 | 2999 | 371 | 151 |
| 0 | 23.9 | 30.5 | 17.1 | 13.4 | 684 | 173 | 1 |
| 0 | 15.0 | 27.2 | -0.5 | 27.7 | 350 | 86 | 0 |
| 0 | 25.3 | 31.8 | 18.9 | 12.9 | 1692 | 285 | 23 |
| 0 | 26.9 | 34.6 | 18.3 | 16.3 | 1664 | 289 | 3 |
| 0 | 22.9 | 30.2 | 15.1 | 15.1 | 1812 | 326 | 4 |
| 0 | 14.2 | 31.2 | -0.5 | 31.7 | 245 | 33 | 11 |
| 0 | 26.8 | 32.6 | 22.7 | 9.9 | 2868 | 442 | 14 |
| 0 | 21.8 | 30.0 | 13.1 | 16.9 | 901 | 161 | 12 |
| 0 | 25.8 | 33.3 | 17.7 | 15.6 | 1357 | 261 | 1 |
| 0 | 25.1 | 31.7 | 18.8 | 12.9 | 2903 | 491 | 42 |
| 0 | 22.8 | 30.5 | 13.1 | 17.4 | 1416 | 199 | 37 |
| 0 | 18.3 | 28.3 | 9.1 | 19.2 | 1846 | 194 | 119 |
| 0 | 26.3 | 32.2 | 21.0 | 11.2 | 1944 | 340 | 38 |
| 0 | 18.8 | 32.5 | 5.3 | 27.2 | 895 | 132 | 19 |
| 0 | 20.6 | 28.8 | 9.6 | 19.2 | 1426 | 276 | 15 |
| 0 | 26.5 | 35.1 | 17.6 | 17.5 | 1650 | 268 | 4 |
| 0 | 25.2 | 35.0 | 16.1 | 18.9 | 2372 | 382 | 9 |
| 0 | 26.2 | 31.8 | 20.4 | 11.4 | 2089 | 226 | 111 |
| 0 | 13.6 | 24.6 | -0.4 | 25.0 | 510 | 175 | 1 |
| 0 | 9.6 | 22.6 | -0.9 | 23.5 | 211 | 27 | 9 |
| 0 | 25.9 | 34.4 | 17.3 | 17.1 | 1782 | 281 | 8 |
| 0 | 25.8 | 31.4 | 20.1 | 11.3 | 2763 | 310 | 140 |
| 0 | 18.9 | 27.0 | 10.2 | 16.8 | 1354 | 217 | 35 |
| 0 | 22.6 | 31.9 | 14.7 | 17.2 | 24 | 19 | 0 |
| 0 | 22.2 | 31.2 | 14.4 | 16.8 | 49 | 17 | 0 |
| 0 | 8.1 | 20.4 | -3.4 | 23.8 | 161 | 24 | 8 |
| 0 | 24.8 | 31.3 | 18.4 | 12.9 | 1811 | 299 | 23 |
| 0 | 23.8 | 30.6 | 16.1 | 14.5 | 1384 | 281 | 6 |
| 0 | 10.3 | 18.9 | 3.6 | 15.3 | 2728 | 361 | 134 |
| 0 | 26.7 | 32.9 | 21.6 | 11.3 | 1822 | 292 | 40 |
| 0 | 24.6 | 31.5 | 16.2 | 15.3 | 1766 | 255 | 54 |
| 0 | 26.6 | 34.4 | 19.5 | 14.9 | 1062 | 265 | 3 |
| 0 | 26.9 | 32.9 | 21.1 | 11.8 | 2315 | 444 | 36 |
| 0 | 25.2 | 33.5 | 16.5 | 17.0 | 1472 | 255 | 14 |
| 0 | 26.2 | 34.4 | 16.5 | 17.9 | 1220 | 210 | 21 |
| 0 | 11.4 | 26.8 | -1.4 | 28.2 | 179 | 20 | 11 |
| 0 | 21.2 | 28.1 | 15.1 | 13.0 | 3403 | 442 | 114 |
| 0 | 20.7 | 35.8 | 5.9 | 29.9 | 651 | 107 | 8 |
| 0 | 15.0 | 30.9 | 1.1 | 29.8 | 273 | 35 | 8 |
| 0 | 5.8 | 16.2 | -6.5 | 22.7 | 757 | 154 | 7 |
| 0 | 5.7 | 18.2 | -9.9 | 28.1 | 64 | 28 | 0 |
| 0 | 25.6 | 31.3 | 19.9 | 11.4 | 1635 | 433 | 7 |
| 0 | 26.0 | 31.5 | 20.0 | 11.5 | 1044 | 179 | 9 |
| 0 | 23.5 | 29.1 | 18.2 | 10.9 | 2969 | 371 | 188 |
| 0 | 26.8 | 33.8 | 21.6 | 12.2 | 3059 | 434 | 72 |
| 0 | 21.1 | 31.4 | 9.3 | 22.1 | 1614 | 186 | 87 |
| 0 | 13.4 | 29.9 | -0.3 | 30.2 | 160 | 26 | 7 |
| 0 | 25.6 | 33.9 | 16.7 | 17.2 | 1459 | 239 | 12 |
| 0 | 22.9 | 31.6 | 12.1 | 19.5 | 1173 | 267 | 4 |
| 0 | 18.3 | 31.5 | 7.1 | 24.4 | 1476 | 146 | 99 |
| 0 | 25.0 | 31.4 | 17.7 | 13.7 | 2897 | 393 | 102 |
| 0 | 26.2 | 31.8 | 20.4 | 11.4 | 2100 | 232 | 109 |
| 0 | 16.3 | 25.8 | 7.5 | 18.3 | 33 | 10 | 0 |
| 0 | 15.6 | 23.2 | 4.8 | 18.4 | 1777 | 322 | 30 |
| 0 | 6.9 | 19.2 | -2.5 | 21.7 | 943 | 133 | 40 |
| 0 | 5.3 | 13.1 | -1.2 | 14.3 | 823 | 83 | 51 |
| 0 | 21.1 | 29.5 | 10.6 | 18.9 | 1269 | 228 | 28 |
| 0 | 22.5 | 34.8 | 8.5 | 26.3 | 701 | 138 | 2 |
| 0 | 20.7 | 32.0 | 8.1 | 23.9 | 1742 | 210 | 82 |
| 0 | 26.0 | 34.9 | 16.9 | 18.0 | 1656 | 270 | 3 |
| 0 | 27.0 | 33.2 | 21.7 | 11.5 | 2110 | 412 | 67 |
| 0 | 16.9 | 31.7 | 3.7 | 28.0 | 800 | 113 | 17 |
| 0 | 19.8 | 28.4 | 12.1 | 16.3 | 1361 | 202 | 22 |
| 0 | 26.2 | 31.5 | 20.7 | 10.8 | 2840 | 296 | 176 |
| 0 | 25.2 | 35.8 | 14.5 | 21.3 | 2314 | 392 | 3 |
| 0 | 20.4 | 28.2 | 9.9 | 18.3 | 1374 | 260 | 18 |
| 0 | 14.0 | 28.0 | 0.4 | 27.6 | 694 | 111 | 12 |
| 0 | 26.2 | 34.2 | 18.7 | 15.5 | 1087 | 182 | 3 |
| 0 | 18.9 | 27.9 | 8.4 | 19.5 | 1305 | 197 | 49 |
| 0 | 12.2 | 25.0 | -3.3 | 28.3 | 278 | 76 | 0 |
| 0 | 23.0 | 30.9 | 15.6 | 15.3 | 1408 | 310 | 3 |
| 0 | 26.4 | 35.2 | 17.4 | 17.8 | 1627 | 265 | 3 |
| 0 | 21.6 | 35.7 | 7.4 | 28.3 | 606 | 113 | 6 |
| 0 | 17.8 | 31.2 | 4.1 | 27.1 | 831 | 132 | 14 |
| 0 | 27.3 | 32.5 | 22.5 | 10.0 | 1897 | 274 | 70 |
| 0 | 26.6 | 32.4 | 21.0 | 11.4 | 1805 | 291 | 51 |
| 0 | 25.6 | 30.6 | 20.5 | 10.1 | 3235 | 355 | 179 |
| 0 | 25.8 | 31.0 | 20.6 | 10.4 | 3529 | 392 | 223 |
| 0 | 26.4 | 33.0 | 21.2 | 11.8 | 1841 | 329 | 53 |
| 0 | 22.0 | 27.4 | 16.9 | 10.5 | 954 | 113 | 41 |
| 0 | 25.1 | 33.3 | 16.2 | 17.1 | 518 | 125 | 1 |
| 0 | 26.7 | 32.2 | 21.3 | 10.9 | 2705 | 350 | 164 |
| 0 | 26.3 | 32.4 | 21.9 | 10.5 | 2394 | 329 | 65 |
| 0 | 26.0 | 32.6 | 20.8 | 11.8 | 3636 | 583 | 62 |
| 0 | 26.0 | 32.5 | 21.1 | 11.4 | 2956 | 432 | 40 |
| 0 | 25.2 | 34.2 | 16.6 | 17.6 | 2288 | 356 | 17 |
| 0 | 27.7 | 35.5 | 21.9 | 13.6 | 1787 | 384 | 2 |
| 0 | 25.5 | 31.4 | 19.0 | 12.4 | 2518 | 290 | 82 |
| 0 | 25.0 | 32.5 | 15.5 | 17.0 | 1235 | 210 | 37 |
| 0 | 24.3 | 31.7 | 15.1 | 16.6 | 1458 | 265 | 5 |
| 0 | 25.3 | 35.8 | 15.5 | 20.3 | 2383 | 386 | 9 |
| 0 | 20.9 | 27.9 | 13.3 | 14.6 | 1118 | 155 | 17 |
| 0 | 25.6 | 31.4 | 19.6 | 11.8 | 2743 | 337 | 86 |
| 0 | 26.3 | 32.5 | 21.6 | 10.9 | 2316 | 341 | 51 |
| 0 | 26.6 | 32.4 | 20.6 | 11.8 | 1297 | 181 | 30 |
| 0 | 23.0 | 31.2 | 13.2 | 18.0 | 1197 | 275 | 4 |
| 0 | 23.4 | 32.1 | 13.6 | 18.5 | 952 | 231 | 1 |
| 0 | 22.9 | 29.3 | 17.1 | 12.2 | 636 | 177 | 2 |
| 0 | 22.3 | 31.1 | 12.5 | 18.6 | 1961 | 336 | 6 |
| 0 | 25.0 | 33.4 | 16.5 | 16.9 | 2086 | 334 | 10 |
| 0 | 26.2 | 31.8 | 20.9 | 10.9 | 3405 | 380 | 223 |
| 0 | 21.9 | 34.4 | 9.4 | 25.0 | 946 | 148 | 19 |
| 0 | 26.0 | 32.5 | 20.3 | 12.2 | 1280 | 206 | 20 |
| 0 | 24.0 | 29.7 | 18.5 | 11.2 | 2302 | 336 | 95 |
| 0 | 27.2 | 34.3 | 21.7 | 12.6 | 3019 | 465 | 70 |
| 0 | 26.2 | 31.7 | 20.6 | 11.1 | 2845 | 328 | 126 |
| 0 | 26.5 | 33.1 | 21.8 | 11.3 | 2484 | 362 | 78 |
| 0 | 25.7 | 34.7 | 16.3 | 18.4 | 1648 | 264 | 4 |
| 0 | 21.2 | 28.5 | 13.5 | 15.0 | 821 | 142 | 19 |
| 0 | 20.1 | 27.0 | 10.6 | 16.4 | 1615 | 295 | 12 |
| 0 | 13.7 | 18.7 | 8.9 | 9.8 | 1287 | 179 | 60 |
| 0 | 15.8 | 30.1 | 1.7 | 28.4 | 724 | 115 | 13 |
| 0 | 26.6 | 33.1 | 21.1 | 12.0 | 2810 | 360 | 66 |
| 0 | 25.3 | 33.5 | 14.9 | 18.6 | 1501 | 278 | 15 |
| 0 | 16.5 | 21.6 | 11.7 | 9.9 | 2079 | 231 | 116 |
| 0 | 27.8 | 35.6 | 21.8 | 13.8 | 2296 | 396 | 12 |
| 0 | 26.9 | 33.0 | 21.4 | 11.6 | 2305 | 323 | 80 |
| 0 | 18.0 | 29.3 | 6.0 | 23.3 | 1881 | 206 | 115 |
| 0 | 24.9 | 34.1 | 14.6 | 19.5 | 1294 | 173 | 47 |
| 0 | 13.0 | 29.9 | -0.7 | 30.6 | 174 | 29 | 6 |
| 0 | 26.5 | 34.8 | 18.3 | 16.5 | 1519 | 255 | 10 |
| 0 | 24.8 | 32.4 | 17.2 | 15.2 | 1584 | 299 | 3 |
| 0 | 25.9 | 34.1 | 17.0 | 17.1 | 1563 | 256 | 22 |
| 0 | 26.5 | 31.9 | 21.5 | 10.4 | 1671 | 243 | 71 |
| 0 | 8.6 | 22.1 | -0.3 | 22.4 | 1543 | 265 | 45 |
| 0 | 15.1 | 32.0 | 1.5 | 30.5 | 685 | 90 | 21 |
| 0 | 23.4 | 30.5 | 16.9 | 13.6 | 748 | 194 | 2 |
| 0 | 13.2 | 29.4 | -0.3 | 29.7 | 142 | 17 | 7 |
| 0 | 18.5 | 34.2 | 2.3 | 31.9 | 235 | 52 | 3 |
| 0 | 25.8 | 32.3 | 20.4 | 11.9 | 3335 | 409 | 145 |
| 0 | 25.6 | 31.2 | 20.4 | 10.8 | 3460 | 409 | 221 |
| 0 | 24.9 | 33.8 | 15.1 | 18.7 | 1918 | 336 | 5 |
| 0 | 14.6 | 32.0 | -0.7 | 32.7 | 264 | 37 | 10 |
| 0 | 24.6 | 30.9 | 19.8 | 11.1 | 1710 | 266 | 37 |
| 0 | 20.2 | 34.6 | 6.7 | 27.9 | 894 | 127 | 17 |
| 0 | 17.5 | 31.0 | 4.0 | 27.0 | 821 | 132 | 13 |
| 0 | 14.1 | 27.5 | 3.3 | 24.2 | 313 | 80 | 0 |
| 0 | 26.5 | 33.8 | 19.2 | 14.6 | 2302 | 318 | 41 |
| 0 | 26.0 | 33.8 | 17.9 | 15.9 | 1258 | 254 | 9 |
| 0 | 18.5 | 28.4 | 9.2 | 19.2 | 1922 | 193 | 126 |
| 0 | 26.1 | 33.6 | 17.1 | 16.5 | 1531 | 306 | 5 |
| 0 | 20.3 | 28.4 | 10.6 | 17.8 | 1508 | 336 | 10 |
| 0 | 26.9 | 33.1 | 21.0 | 12.1 | 2214 | 431 | 22 |
| 0 | 26.3 | 33.4 | 19.4 | 14.0 | 995 | 179 | 5 |
| 0 | 26.8 | 34.8 | 19.2 | 15.6 | 927 | 156 | 2 |
| 0 | 26.7 | 32.9 | 22.0 | 10.9 | 2199 | 323 | 83 |
| 0 | 26.2 | 33.7 | 17.7 | 16.0 | 1548 | 315 | 4 |
| 0 | 23.8 | 32.9 | 13.6 | 19.3 | 1388 | 183 | 48 |
| 0 | 22.2 | 28.1 | 16.6 | 11.5 | 2074 | 352 | 62 |
| 0 | 25.8 | 33.8 | 18.8 | 15.0 | 1470 | 333 | 0 |
| 0 | 26.8 | 33.1 | 20.8 | 12.3 | 2254 | 319 | 69 |
| 0 | 18.5 | 28.8 | 9.8 | 19.0 | 1427 | 133 | 104 |
| 0 | 27.1 | 32.7 | 22.3 | 10.4 | 2199 | 280 | 83 |
| 0 | 26.8 | 32.4 | 21.5 | 10.9 | 2686 | 372 | 140 |
| 0 | 22.8 | 30.3 | 13.6 | 16.7 | 1597 | 287 | 15 |
| 0 | 21.1 | 30.3 | 10.3 | 20.0 | 1385 | 159 | 59 |
| 0 | 5.3 | 16.3 | -3.4 | 19.7 | 991 | 135 | 41 |
| 0 | 22.4 | 29.6 | 15.7 | 13.9 | 2875 | 487 | 31 |
| 0 | 25.1 | 34.8 | 16.0 | 18.8 | 2342 | 377 | 9 |
| 0 | 26.0 | 33.8 | 17.7 | 16.1 | 1675 | 310 | 3 |
| 0 | 4.0 | 11.8 | -2.5 | 14.3 | 1880 | 180 | 133 |
| 0 | 26.7 | 32.7 | 22.5 | 10.2 | 2318 | 336 | 50 |
| 0 | 26.5 | 33.9 | 20.1 | 13.8 | 3991 | 655 | 88 |
| 0 | 25.8 | 32.3 | 18.7 | 13.6 | 2182 | 299 | 33 |
| 0 | 19.4 | 32.6 | 8.0 | 24.6 | 1166 | 141 | 52 |
| 0 | 26.2 | 31.1 | 21.6 | 9.5 | 2714 | 380 | 102 |
| 0 | 27.4 | 33.8 | 21.9 | 11.9 | 2238 | 301 | 29 |
| 0 | 20.7 | 35.2 | 5.1 | 30.1 | 576 | 115 | 5 |
| 0 | 24.5 | 32.3 | 14.6 | 17.7 | 1415 | 264 | 9 |
| 0 | 23.1 | 30.6 | 16.5 | 14.1 | 515 | 80 | 12 |
| 0 | 26.3 | 31.7 | 20.8 | 10.9 | 2823 | 339 | 105 |
| 0 | 26.2 | 33.2 | 19.5 | 13.7 | 1716 | 289 | 19 |
| 0 | 27.8 | 35.2 | 21.2 | 14.0 | 1101 | 283 | 0 |
| 0 | 20.6 | 26.8 | 14.6 | 12.2 | 718 | 113 | 24 |
| 0 | 10.4 | 21.0 | -1.7 | 22.7 | 16 | 11 | 0 |
| 0 | 26.7 | 35.1 | 18.0 | 17.1 | 1764 | 283 | 3 |
| 0 | 26.9 | 32.5 | 22.0 | 10.5 | 2794 | 420 | 121 |
| 0 | 23.9 | 32.4 | 13.5 | 18.9 | 1384 | 200 | 35 |
| 0 | 22.0 | 30.6 | 11.7 | 18.9 | 1060 | 227 | 2 |
| 0 | 27.2 | 35.0 | 18.5 | 16.5 | 1658 | 329 | 1 |
| 0 | 25.4 | 34.0 | 15.4 | 18.6 | 1647 | 290 | 2 |
| 0 | 21.8 | 29.1 | 15.5 | 13.6 | 3204 | 527 | 50 |
| 0 | 25.6 | 33.6 | 18.2 | 15.4 | 761 | 180 | 1 |
| 0 | 19.9 | 26.6 | 12.6 | 14.0 | 812 | 123 | 33 |
| 0 | 19.0 | 26.8 | 8.2 | 18.6 | 1457 | 259 | 23 |
| 0 | 23.4 | 28.9 | 18.6 | 10.3 | 3172 | 499 | 42 |
| 0 | 27.2 | 35.6 | 18.7 | 16.9 | 789 | 162 | 2 |
| 0 | 10.6 | 26.4 | -3.4 | 29.8 | 408 | 58 | 21 |
| 0 | 15.2 | 32.5 | 0.5 | 32.0 | 303 | 39 | 13 |
| 0 | 23.6 | 33.7 | 10.9 | 22.8 | 1037 | 229 | 3 |
| 0 | 24.0 | 31.9 | 16.2 | 15.7 | 1486 | 286 | 1 |
| 0 | 20.3 | 29.1 | 9.9 | 19.2 | 1235 | 238 | 17 |
| 0 | 17.3 | 30.3 | 6.9 | 23.4 | 1205 | 116 | 84 |
| 0 | 24.5 | 32.6 | 14.0 | 18.6 | 1175 | 236 | 3 |
| 0 | 26.3 | 33.3 | 21.0 | 12.3 | 2886 | 382 | 54 |
| 0 | 11.4 | 23.3 | -1.8 | 25.1 | 142 | 36 | 0 |
| 0 | 22.3 | 29.5 | 15.2 | 14.3 | 760 | 97 | 23 |
| 0 | 26.8 | 33.5 | 20.8 | 12.7 | 1620 | 340 | 16 |
| 0 | 26.1 | 32.8 | 19.2 | 13.6 | 2032 | 287 | 23 |
| 0 | 23.1 | 29.9 | 17.1 | 12.8 | 3427 | 608 | 68 |
| 0 | 22.8 | 31.4 | 12.4 | 19.0 | 1169 | 274 | 3 |
| 0 | 21.4 | 36.2 | 7.0 | 29.2 | 661 | 110 | 8 |
| 0 | 8.7 | 16.0 | 2.7 | 13.3 | 2452 | 266 | 155 |
| 0 | 24.2 | 32.4 | 16.2 | 16.2 | 1632 | 285 | 1 |
| 0 | 27.3 | 33.4 | 22.6 | 10.8 | 2338 | 382 | 77 |
| 0 | 26.9 | 32.4 | 22.0 | 10.4 | 2582 | 351 | 126 |
| 0 | 16.1 | 32.5 | 0.2 | 32.3 | 479 | 77 | 8 |
| 0 | 23.9 | 35.2 | 12.9 | 22.3 | 1132 | 149 | 24 |
| 0 | 26.3 | 32.1 | 20.8 | 11.3 | 3505 | 396 | 229 |
| 0 | 22.9 | 31.0 | 12.1 | 18.9 | 1239 | 257 | 3 |
| 0 | 25.3 | 34.5 | 15.5 | 19.0 | 830 | 160 | 1 |
| 0 | 25.0 | 32.6 | 14.9 | 17.7 | 1896 | 313 | 47 |
| 0 | 26.4 | 33.4 | 19.3 | 14.1 | 1670 | 276 | 13 |
| 0 | 25.7 | 31.1 | 20.1 | 11.0 | 2837 | 321 | 157 |
| 0 | 17.6 | 29.9 | 7.6 | 22.3 | 1228 | 122 | 76 |
| 0 | -2.2 | 8.3 | -12.0 | 20.3 | 155 | 27 | 7 |
| 0 | 27.5 | 35.7 | 20.9 | 14.8 | 1463 | 259 | 6 |
| 0 | 18.8 | 27.0 | 10.3 | 16.7 | 952 | 152 | 24 |
| 0 | 20.6 | 27.2 | 14.8 | 12.4 | 776 | 132 | 15 |
| 0 | 3.1 | 13.2 | -8.5 | 21.7 | 38 | 12 | 0 |
| 0 | 25.5 | 33.6 | 17.0 | 16.6 | 2260 | 369 | 10 |
| 0 | 25.2 | 34.0 | 16.2 | 17.8 | 1325 | 252 | 11 |
| 0 | 25.8 | 33.8 | 16.6 | 17.2 | 1738 | 289 | 34 |
| 0 | 26.3 | 33.2 | 21.1 | 12.1 | 1841 | 340 | 42 |
| 0 | 25.7 | 30.9 | 21.0 | 9.9 | 5870 | 651 | 257 |
| 0 | 21.0 | 26.8 | 15.6 | 11.2 | 1669 | 233 | 66 |
| 0 | 24.3 | 33.4 | 13.4 | 20.0 | 1087 | 188 | 20 |
| 0 | 23.9 | 31.6 | 14.3 | 17.3 | 1500 | 251 | 31 |
| 0 | 22.5 | 30.6 | 12.3 | 18.3 | 1668 | 272 | 14 |
| 0 | 9.7 | 17.5 | 0.4 | 17.1 | 1338 | 193 | 39 |
| 0 | 24.2 | 30.6 | 19.4 | 11.2 | 2145 | 316 | 53 |
| 0 | 23.5 | 31.1 | 13.2 | 17.9 | 1245 | 195 | 25 |
| 0 | 19.4 | 30.4 | 8.7 | 21.7 | 1960 | 197 | 141 |
| 0 | 26.6 | 34.4 | 18.8 | 15.6 | 1653 | 255 | 14 |
| 0 | 18.3 | 31.9 | 4.6 | 27.3 | 845 | 131 | 15 |
| 0 | 19.2 | 27.3 | 10.4 | 16.9 | 1596 | 267 | 33 |
| 0 | 22.1 | 31.6 | 11.2 | 20.4 | 1406 | 180 | 61 |
| 0 | 16.1 | 32.3 | 2.2 | 30.1 | 697 | 100 | 23 |
| 0 | 10.7 | 23.4 | 0.3 | 23.1 | 205 | 26 | 10 |
| 0 | 22.8 | 30.7 | 11.7 | 19.0 | 1276 | 231 | 23 |
| 0 | 25.3 | 32.2 | 20.2 | 12.0 | 2269 | 362 | 53 |
| 0 | 26.3 | 34.3 | 18.4 | 15.9 | 1414 | 236 | 3 |
| 0 | 26.4 | 31.8 | 20.8 | 11.0 | 2764 | 316 | 135 |
| 0 | 26.8 | 32.9 | 20.4 | 12.5 | 2465 | 255 | 124 |
| 0 | 26.6 | 34.7 | 17.9 | 16.8 | 1511 | 259 | 2 |
| 0 | 26.0 | 32.4 | 20.1 | 12.3 | 1893 | 301 | 52 |
| 0 | 17.7 | 26.6 | 9.5 | 17.1 | 1 | 1 | 0 |
| 0 | 7.3 | 17.2 | -4.2 | 21.4 | 21 | 7 | 0 |
| 0 | 22.2 | 32.1 | 12.1 | 20.0 | 1469 | 159 | 61 |
| 0 | 15.9 | 32.4 | 0.0 | 32.4 | 463 | 74 | 7 |
| 0 | 24.4 | 32.7 | 16.4 | 16.3 | 2075 | 327 | 21 |
| 0 | 16.7 | 27.7 | 7.7 | 20.0 | 1150 | 110 | 82 |
| 0 | 26.1 | 35.1 | 16.6 | 18.5 | 1561 | 272 | 2 |
| 0 | 26.6 | 33.4 | 19.7 | 13.7 | 2294 | 312 | 43 |
| 0 | 23.3 | 29.5 | 17.5 | 12.0 | 995 | 137 | 44 |
| 0 | 27.1 | 33.5 | 21.1 | 12.4 | 774 | 182 | 3 |
| 0 | 27.0 | 32.7 | 21.4 | 11.3 | 1790 | 358 | 43 |
| 0 | 27.7 | 34.9 | 21.1 | 13.8 | 1058 | 162 | 7 |
| 0 | 17.2 | 29.4 | 6.5 | 22.9 | 950 | 108 | 59 |
| 0 | 1.0 | 8.5 | -9.5 | 18.0 | 946 | 170 | 7 |
| 0 | 26.8 | 33.4 | 21.0 | 12.4 | 2571 | 328 | 46 |
| 0 | 21.6 | 34.7 | 7.4 | 27.3 | 636 | 128 | 3 |
| 0 | 23.7 | 30.9 | 15.3 | 15.6 | 1635 | 318 | 5 |
| 0 | 26.7 | 32.9 | 21.1 | 11.8 | 2466 | 419 | 51 |
| 0 | 18.8 | 28.1 | 7.9 | 20.2 | 1464 | 196 | 67 |
| 0 | 27.0 | 32.8 | 22.2 | 10.6 | 2244 | 338 | 84 |
| 0 | 21.3 | 32.4 | 10.3 | 22.1 | 1582 | 193 | 82 |
| 0 | 27.6 | 35.2 | 21.5 | 13.7 | 1625 | 272 | 8 |
| 0 | 21.7 | 34.3 | 9.2 | 25.1 | 1120 | 142 | 25 |
| 0 | 26.4 | 33.7 | 19.2 | 14.5 | 2172 | 308 | 25 |
| 0 | 26.8 | 32.8 | 21.1 | 11.7 | 2273 | 443 | 39 |
| 0 | 24.8 | 32.9 | 16.5 | 16.4 | 2086 | 339 | 22 |
| 0 | 25.7 | 33.8 | 18.7 | 15.1 | 2498 | 459 | 18 |
| 0 | 17.5 | 25.4 | 7.9 | 17.5 | 1378 | 202 | 40 |
| 0 | 25.0 | 34.6 | 13.9 | 20.7 | 767 | 112 | 13 |
| 0 | 23.8 | 32.5 | 14.3 | 18.2 | 1609 | 275 | 9 |
| 0 | 25.1 | 31.1 | 19.5 | 11.6 | 2711 | 344 | 60 |
| 0 | -0.4 | 6.6 | -6.8 | 13.4 | 1619 | 166 | 94 |
| 0 | 23.7 | 31.6 | 16.2 | 15.4 | 450 | 100 | 7 |
| 0 | 25.4 | 32.9 | 15.4 | 17.5 | 2618 | 418 | 78 |
| 0 | 26.5 | 32.0 | 21.5 | 10.5 | 2225 | 267 | 77 |
| 0 | 26.2 | 34.1 | 18.6 | 15.5 | 1454 | 260 | 9 |
| 0 | 27.0 | 34.2 | 21.1 | 13.1 | 3276 | 462 | 82 |
| 0 | 25.6 | 34.3 | 15.4 | 18.9 | 1121 | 168 | 28 |
| 0 | 26.6 | 35.0 | 18.9 | 16.1 | 1149 | 286 | 3 |
| 0 | 6.4 | 21.8 | -5.6 | 27.4 | 185 | 28 | 7 |
| 0 | 22.8 | 32.0 | 13.3 | 18.7 | 1963 | 324 | 9 |
| 0 | 22.6 | 30.4 | 12.9 | 17.5 | 1455 | 237 | 31 |
| 0 | 10.8 | 21.6 | -1.7 | 23.3 | 25 | 12 | 0 |
| 0 | 25.5 | 32.6 | 17.5 | 15.1 | 1844 | 298 | 55 |
| 0 | 18.0 | 29.3 | 8.5 | 20.8 | 1364 | 132 | 90 |
| 0 | 22.6 | 34.6 | 10.2 | 24.4 | 923 | 124 | 18 |
| 0 | -4.3 | 8.9 | -15.6 | 24.5 | 446 | 97 | 12 |
| 0 | 25.5 | 32.6 | 19.7 | 12.9 | 2547 | 389 | 51 |
| 0 | 19.9 | 28.9 | 9.4 | 19.5 | 1264 | 230 | 18 |
| 0 | 26.1 | 32.9 | 19.0 | 13.9 | 1789 | 267 | 14 |
| 0 | 26.3 | 34.2 | 18.8 | 15.4 | 1216 | 240 | 3 |
| 0 | 23.1 | 30.7 | 15.9 | 14.8 | 796 | 106 | 30 |
| 0 | 24.1 | 31.4 | 16.9 | 14.5 | 808 | 184 | 9 |
| 0 | 24.6 | 33.1 | 15.0 | 18.1 | 897 | 155 | 31 |
| 0 | 22.1 | 34.4 | 7.8 | 26.6 | 680 | 137 | 2 |
| 0 | 7.6 | 21.3 | -9.6 | 30.9 | 156 | 51 | 0 |
| 0 | 25.3 | 31.5 | 19.3 | 12.2 | 1922 | 334 | 24 |
| 0 | 19.1 | 33.7 | 2.4 | 31.3 | 370 | 81 | 6 |
| 0 | 23.0 | 31.4 | 11.5 | 19.9 | 1034 | 227 | 2 |
| 0 | 17.9 | 28.2 | 7.2 | 21.0 | 1454 | 163 | 82 |
| 0 | 25.6 | 31.8 | 20.4 | 11.4 | 3040 | 369 | 90 |
| 0 | 18.1 | 25.7 | 9.1 | 16.6 | 964 | 146 | 30 |
| 0 | 25.2 | 33.2 | 18.2 | 15.0 | 559 | 150 | 3 |
| 0 | 25.0 | 33.6 | 16.4 | 17.2 | 1811 | 288 | 7 |
| 0 | 27.3 | 32.8 | 21.8 | 11.0 | 1822 | 308 | 68 |
| 0 | 25.6 | 32.0 | 18.1 | 13.9 | 1951 | 269 | 34 |
| 0 | 24.9 | 33.1 | 16.0 | 17.1 | 491 | 114 | 2 |
| 0 | 20.0 | 28.7 | 8.3 | 20.4 | 1412 | 272 | 17 |
| 0 | 10.8 | 25.2 | -0.8 | 26.0 | 177 | 24 | 9 |
| 0 | 25.8 | 33.6 | 16.0 | 17.6 | 1356 | 235 | 30 |
| 0 | 17.9 | 32.2 | 6.2 | 26.0 | 1036 | 148 | 40 |
| 0 | 27.1 | 32.6 | 21.7 | 10.9 | 2363 | 353 | 108 |
| 0 | 26.4 | 32.6 | 22.0 | 10.6 | 2573 | 370 | 28 |
| 0 | 19.8 | 31.4 | 9.0 | 22.4 | 1677 | 184 | 110 |
| 0 | 26.5 | 33.6 | 19.3 | 14.3 | 2163 | 318 | 39 |
| 0 | 19.9 | 27.7 | 9.3 | 18.4 | 1303 | 240 | 22 |
| 0 | 21.6 | 28.8 | 14.5 | 14.3 | 902 | 222 | 7 |
| 0 | 13.0 | 24.5 | -1.8 | 26.3 | 371 | 96 | 1 |
| 0 | 24.8 | 33.4 | 16.5 | 16.9 | 1740 | 280 | 14 |
| 0 | 7.3 | 19.9 | -8.1 | 28.0 | 92 | 33 | 0 |
| 0 | 26.4 | 31.8 | 21.0 | 10.8 | 2871 | 320 | 165 |
| 0 | 25.3 | 32.2 | 17.5 | 14.7 | 1855 | 243 | 37 |
| 0 | 26.8 | 32.4 | 21.5 | 10.9 | 3263 | 355 | 203 |
| 0 | 26.7 | 33.1 | 20.2 | 12.9 | 1062 | 188 | 8 |
| 0 | 25.9 | 34.5 | 17.4 | 17.1 | 1459 | 245 | 7 |
| 0 | 18.9 | 24.7 | 12.9 | 11.8 | 1726 | 262 | 38 |
| 0 | 23.5 | 34.7 | 12.1 | 22.6 | 936 | 129 | 25 |
| 0 | 23.4 | 32.2 | 14.4 | 17.8 | 1445 | 236 | 1 |
| 0 | 22.4 | 28.4 | 16.7 | 11.7 | 2464 | 335 | 133 |
| 0 | 24.8 | 34.0 | 14.4 | 19.6 | 665 | 107 | 12 |
| 0 | 26.4 | 31.8 | 21.4 | 10.4 | 2784 | 337 | 161 |
| 0 | 26.3 | 32.6 | 21.4 | 11.2 | 2273 | 463 | 5 |
| 0 | 23.9 | 31.2 | 14.0 | 17.2 | 1332 | 222 | 26 |
| 0 | 25.2 | 32.3 | 17.3 | 15.0 | 2001 | 257 | 52 |
| 0 | 26.5 | 32.8 | 20.7 | 12.1 | 2529 | 321 | 49 |
| 0 | 6.8 | 17.5 | -2.5 | 20.0 | 419 | 50 | 23 |
| 0 | 15.5 | 24.5 | 7.0 | 17.5 | 1664 | 206 | 99 |
| 0 | 27.4 | 33.4 | 22.9 | 10.5 | 2236 | 323 | 63 |
| 0 | 25.9 | 33.3 | 17.8 | 15.5 | 1794 | 294 | 46 |
| 0 | 18.7 | 31.6 | 7.7 | 23.9 | 1508 | 147 | 103 |
| 0 | 14.7 | 28.2 | 3.5 | 24.7 | 623 | 66 | 40 |
| 0 | 19.8 | 31.2 | 8.7 | 22.5 | 1785 | 181 | 119 |
| 0 | 17.9 | 31.4 | 6.5 | 24.9 | 1412 | 145 | 93 |
| 0 | 18.5 | 28.4 | 7.1 | 21.3 | 1462 | 173 | 80 |
| 0 | 27.1 | 34.0 | 20.1 | 13.9 | 1067 | 194 | 5 |
| 0 | 17.4 | 30.9 | 6.3 | 24.6 | 1243 | 123 | 71 |
| 0 | 17.6 | 25.6 | 8.9 | 16.7 | 6 | 2 | 0 |
| 0 | 27.7 | 34.9 | 22.4 | 12.5 | 2914 | 424 | 46 |
| 0 | 3.4 | 14.4 | -12.1 | 26.5 | 772 | 150 | 5 |
| 0 | 26.6 | 34.0 | 21.4 | 12.6 | 2827 | 428 | 28 |
| 0 | 21.2 | 27.5 | 14.1 | 13.4 | 589 | 120 | 7 |
| 0 | 24.5 | 32.7 | 14.5 | 18.2 | 1088 | 182 | 22 |
| 0 | 27.0 | 33.3 | 22.1 | 11.2 | 2328 | 369 | 65 |
| 0 | 12.0 | 28.4 | -2.6 | 31.0 | 228 | 24 | 15 |
| 0 | 10.5 | 23.0 | 0.4 | 22.6 | 200 | 26 | 10 |
| 0 | 25.8 | 31.5 | 19.9 | 11.6 | 493 | 137 | 1 |
| 0 | 26.9 | 32.9 | 22.0 | 10.9 | 2599 | 341 | 86 |
| 0 | 12.2 | 22.0 | 2.7 | 19.3 | 32 | 11 | 0 |
| 0 | 23.6 | 30.2 | 16.4 | 13.8 | 1582 | 268 | 5 |
| 0 | 21.9 | 28.1 | 16.0 | 12.1 | 2779 | 381 | 110 |
| 0 | 23.6 | 30.9 | 14.5 | 16.4 | 1329 | 286 | 5 |
| 0 | 27.3 | 35.1 | 18.9 | 16.2 | 1845 | 333 | 2 |
| 0 | 3.2 | 14.7 | -11.1 | 25.8 | 120 | 50 | 0 |
| 0 | 26.3 | 33.1 | 19.4 | 13.7 | 1364 | 291 | 15 |
| 0 | 23.3 | 31.0 | 13.1 | 17.9 | 1247 | 191 | 26 |
| 0 | 24.2 | 30.7 | 18.0 | 12.7 | 760 | 121 | 21 |
| 0 | 13.7 | 30.2 | 1.7 | 28.5 | 778 | 101 | 25 |
| 0 | 24.7 | 32.7 | 16.5 | 16.2 | 2020 | 314 | 17 |
| 0 | 25.8 | 32.3 | 21.0 | 11.3 | 1830 | 275 | 60 |
| 0 | 24.9 | 33.9 | 15.2 | 18.7 | 1976 | 350 | 6 |
| 0 | 25.9 | 32.9 | 19.8 | 13.1 | 1329 | 290 | 4 |
| 0 | 24.4 | 33.6 | 14.5 | 19.1 | 1974 | 336 | 3 |
| 0 | 21.2 | 36.4 | 6.8 | 29.6 | 672 | 108 | 8 |
| 0 | 20.8 | 28.5 | 13.2 | 15.3 | 1333 | 233 | 17 |
| 0 | 23.9 | 32.2 | 14.9 | 17.3 | 846 | 184 | 0 |
| 0 | 23.9 | 32.1 | 13.5 | 18.6 | 1536 | 270 | 12 |
| 0 | 3.5 | 11.5 | -6.9 | 18.4 | 830 | 172 | 4 |
| 0 | 25.6 | 32.0 | 18.0 | 14.0 | 1836 | 256 | 31 |
| 0 | 28.1 | 33.3 | 22.5 | 10.8 | 574 | 144 | 3 |
| 0 | 26.6 | 33.2 | 20.0 | 13.2 | 2278 | 316 | 53 |
| 0 | 20.9 | 30.9 | 9.8 | 21.1 | 1503 | 167 | 73 |
| 0 | 27.8 | 35.3 | 21.7 | 13.6 | 1491 | 256 | 8 |
| 0 | 26.5 | 32.8 | 21.8 | 11.0 | 2180 | 320 | 51 |
| 0 | 25.7 | 31.5 | 19.9 | 11.6 | 2283 | 224 | 143 |
| 0 | 16.0 | 21.9 | 10.0 | 11.9 | 2074 | 336 | 37 |
| 0 | 26.7 | 33.6 | 20.7 | 12.9 | 3409 | 455 | 142 |
| 0 | 26.0 | 34.2 | 15.9 | 18.3 | 1325 | 216 | 12 |
| 0 | 23.5 | 30.9 | 14.4 | 16.5 | 1432 | 222 | 31 |
| 0 | 25.6 | 34.2 | 17.2 | 17.0 | 1247 | 211 | 0 |
| 0 | 26.0 | 31.5 | 20.9 | 10.6 | 1932 | 273 | 77 |
| 0 | 26.8 | 32.4 | 21.5 | 10.9 | 2251 | 324 | 115 |
| 0 | 16.1 | 29.7 | 2.8 | 26.9 | 757 | 122 | 14 |
| 0 | 17.4 | 28.9 | 7.7 | 21.2 | 1333 | 132 | 79 |
| 0 | 11.0 | 25.2 | -6.8 | 32.0 | 267 | 74 | 0 |
| 0 | 23.6 | 32.6 | 13.4 | 19.2 | 1932 | 339 | 3 |
| 0 | 26.4 | 34.2 | 18.9 | 15.3 | 1302 | 230 | 7 |
| 0 | 5.7 | 13.1 | -0.4 | 13.5 | 572 | 68 | 34 |
| 0 | 13.0 | 26.3 | 2.7 | 23.6 | 431 | 111 | 1 |
| 0 | 27.3 | 35.4 | 20.3 | 15.1 | 1442 | 312 | 6 |
| 0 | 11.7 | 22.4 | -0.2 | 22.6 | 19 | 9 | 0 |
| 0 | 13.1 | 24.9 | 3.7 | 21.2 | 418 | 125 | 0 |
| 0 | 22.4 | 31.0 | 12.6 | 18.4 | 1202 | 252 | 11 |
| 0 | 25.6 | 35.7 | 15.8 | 19.9 | 2355 | 408 | 10 |
| 0 | 26.4 | 32.6 | 20.6 | 12.0 | 2101 | 381 | 25 |
| 0 | 24.7 | 34.1 | 14.0 | 20.1 | 674 | 100 | 11 |
| 0 | 4.4 | 16.0 | -12.3 | 28.3 | 802 | 175 | 3 |
| 0 | 26.1 | 32.9 | 20.9 | 12.0 | 3470 | 549 | 36 |
| 0 | 23.1 | 32.1 | 13.7 | 18.4 | 1718 | 268 | 9 |
| 0 | 21.9 | 32.6 | 11.3 | 21.3 | 1416 | 152 | 73 |
| 0 | 22.9 | 29.1 | 16.3 | 12.8 | 905 | 132 | 35 |
| 0 | 24.1 | 31.5 | 14.9 | 16.6 | 1537 | 278 | 21 |
| 0 | 11.2 | 27.7 | -3.3 | 31.0 | 226 | 24 | 14 |
| 0 | 1.8 | 11.7 | -7.8 | 19.5 | 106 | 14 | 4 |
| 0 | 24.7 | 35.2 | 15.3 | 19.9 | 2424 | 403 | 11 |
| 0 | 27.4 | 34.9 | 21.7 | 13.2 | 2474 | 378 | 15 |
| 0 | 26.1 | 32.6 | 20.8 | 11.8 | 3252 | 398 | 124 |
| 0 | 15.2 | 30.6 | 2.8 | 27.8 | 274 | 71 | 1 |
| 0 | 26.3 | 33.1 | 21.0 | 12.1 | 1831 | 340 | 39 |
| 0 | 24.6 | 33.4 | 14.2 | 19.2 | 1911 | 349 | 2 |
| 0 | 25.0 | 31.8 | 19.3 | 12.5 | 2435 | 378 | 47 |
| 0 | 23.1 | 34.7 | 10.9 | 23.8 | 827 | 103 | 18 |
| 0 | 26.4 | 32.7 | 20.7 | 12.0 | 2003 | 364 | 21 |
| 0 | 23.7 | 31.3 | 14.6 | 16.7 | 1632 | 309 | 7 |
| 0 | 25.5 | 30.8 | 20.3 | 10.5 | 3277 | 343 | 203 |
| 0 | 25.7 | 31.4 | 20.0 | 11.4 | 2655 | 260 | 186 |
| 0 | 25.4 | 31.5 | 18.3 | 13.2 | 2253 | 277 | 58 |
| 0 | 12.2 | 29.0 | -2.8 | 31.8 | 232 | 28 | 11 |
| 0 | 4.5 | 12.7 | -6.3 | 19.0 | 723 | 144 | 2 |
| 0 | 17.4 | 30.5 | 6.8 | 23.7 | 1226 | 118 | 80 |
| 0 | 23.5 | 31.2 | 16.2 | 15.0 | 655 | 85 | 23 |
| 0 | 17.2 | 30.6 | 3.6 | 27.0 | 777 | 130 | 11 |
| 0 | 26.4 | 32.2 | 20.8 | 11.4 | 2756 | 347 | 71 |
| 0 | 23.8 | 31.3 | 14.4 | 16.9 | 1396 | 222 | 28 |
| 0 | 22.7 | 32.4 | 12.6 | 19.8 | 1418 | 158 | 54 |
| 0 | 20.5 | 34.2 | 5.9 | 28.3 | 434 | 87 | 4 |
| 0 | 9.4 | 17.0 | 3.2 | 13.8 | 2758 | 319 | 162 |
| 0 | 22.5 | 34.4 | 9.9 | 24.5 | 912 | 129 | 18 |
| 0 | 26.3 | 32.5 | 21.0 | 11.5 | 2331 | 435 | 35 |
| 0 | 26.2 | 32.3 | 21.6 | 10.7 | 2356 | 338 | 46 |
| 0 | 3.3 | 13.6 | -9.7 | 23.3 | 347 | 91 | 0 |
| 0 | 25.7 | 34.4 | 16.8 | 17.6 | 2428 | 358 | 23 |
| 0 | 25.2 | 31.5 | 19.0 | 12.5 | 1622 | 277 | 28 |
| 0 | 26.0 | 33.0 | 18.8 | 14.2 | 1711 | 273 | 6 |
| 0 | 25.3 | 32.2 | 20.5 | 11.7 | 2341 | 397 | 51 |
| 0 | 23.7 | 32.5 | 13.0 | 19.5 | 1674 | 294 | 4 |
| 0 | 26.1 | 31.8 | 20.2 | 11.6 | 2815 | 254 | 188 |
| 0 | 21.5 | 27.6 | 15.4 | 12.2 | 3391 | 478 | 84 |
| 0 | 22.3 | 30.6 | 11.8 | 18.8 | 1857 | 308 | 10 |
| 0 | 20.0 | 27.9 | 9.5 | 18.4 | 1281 | 234 | 26 |
| 0 | 15.8 | 25.2 | 7.2 | 18.0 | 1921 | 190 | 134 |
| 0 | 26.5 | 34.1 | 19.0 | 15.1 | 1629 | 259 | 12 |
| 0 | 24.6 | 33.1 | 13.8 | 19.3 | 1458 | 255 | 19 |
| 0 | 8.6 | 20.8 | -2.9 | 23.7 | 162 | 24 | 8 |
| 0 | 25.5 | 31.5 | 19.2 | 12.3 | 2666 | 337 | 74 |
| 0 | 22.2 | 30.4 | 11.7 | 18.7 | 1588 | 269 | 11 |
| 0 | 25.2 | 34.3 | 15.4 | 18.9 | 2012 | 349 | 6 |
| 0 | 27.0 | 32.5 | 22.4 | 10.1 | 2969 | 449 | 55 |
| 0 | 18.2 | 31.8 | 4.8 | 27.0 | 891 | 136 | 21 |
| 0 | 23.1 | 31.9 | 12.8 | 19.1 | 877 | 186 | 4 |
| 0 | 26.7 | 33.5 | 20.2 | 13.3 | 1193 | 221 | 3 |
| 0 | 25.4 | 32.1 | 17.7 | 14.4 | 1762 | 243 | 26 |
| 0 | 17.3 | 25.0 | 8.4 | 16.6 | 924 | 146 | 24 |
| 0 | 26.4 | 34.9 | 17.3 | 17.6 | 694 | 133 | 0 |
| 0 | 19.2 | 30.5 | 8.0 | 22.5 | 1895 | 194 | 127 |
| 0 | 26.7 | 32.8 | 21.2 | 11.6 | 1865 | 370 | 46 |
| 0 | 13.8 | 30.9 | -1.1 | 32.0 | 161 | 19 | 9 |
| 0 | 25.3 | 31.5 | 18.3 | 13.2 | 2254 | 279 | 62 |
| 0 | 25.7 | 31.0 | 20.4 | 10.6 | 4478 | 770 | 91 |
| 0 | 23.7 | 29.1 | 17.7 | 11.4 | 1348 | 155 | 84 |
| 0 | 15.9 | 26.0 | 4.9 | 21.1 | 1816 | 191 | 105 |
| 0 | 26.7 | 33.1 | 20.6 | 12.5 | 2257 | 310 | 67 |
| 0 | 25.3 | 33.6 | 15.1 | 18.5 | 1480 | 263 | 23 |
| 0 | 26.6 | 34.6 | 18.6 | 16.0 | 1585 | 262 | 14 |
| 0 | 25.7 | 31.8 | 18.9 | 12.9 | 2465 | 314 | 60 |
| 0 | 25.9 | 31.4 | 20.7 | 10.7 | 2897 | 328 | 166 |
| 0 | 24.0 | 32.6 | 14.4 | 18.2 | 1597 | 273 | 9 |
| 0 | 24.1 | 32.9 | 15.2 | 17.7 | 1469 | 247 | 1 |
| 0 | 6.8 | 18.7 | -4.4 | 23.1 | 144 | 18 | 8 |
| 0 | 19.7 | 27.5 | 9.4 | 18.1 | 1642 | 346 | 15 |
| 0 | 24.9 | 31.8 | 16.5 | 15.3 | 1923 | 285 | 28 |
| 0 | 6.9 | 20.4 | -9.8 | 30.2 | 130 | 43 | 0 |
| 0 | 27.5 | 33.3 | 22.3 | 11.0 | 4153 | 496 | 113 |
| 0 | 26.9 | 35.2 | 18.9 | 16.3 | 759 | 151 | 1 |
| 0 | 17.9 | 32.8 | 0.3 | 32.5 | 173 | 45 | 2 |
| 0 | 20.9 | 29.7 | 10.0 | 19.7 | 1236 | 200 | 30 |
| 0 | 21.9 | 33.5 | 11.3 | 22.2 | 1282 | 168 | 49 |
| 0 | 21.8 | 28.8 | 13.2 | 15.6 | 1407 | 239 | 8 |
| 0 | 27.5 | 34.9 | 21.6 | 13.3 | 3073 | 507 | 46 |
| 0 | 24.5 | 32.3 | 14.6 | 17.7 | 1535 | 258 | 20 |
| 0 | 8.7 | 19.7 | -5.9 | 25.6 | 232 | 83 | 0 |
| 0 | 25.5 | 31.1 | 20.5 | 10.6 | 3215 | 355 | 192 |
| 0 | 17.4 | 24.9 | 6.6 | 18.3 | 1600 | 286 | 26 |
| 0 | 25.9 | 33.4 | 18.3 | 15.1 | 2550 | 388 | 19 |
| 0 | 26.1 | 34.2 | 16.1 | 18.1 | 1304 | 217 | 15 |
| 0 | 15.8 | 25.2 | 7.2 | 18.0 | 0 | 0 | 0 |
| 0 | 7.4 | 20.2 | -4.2 | 24.4 | 189 | 25 | 10 |
| 0 | 21.8 | 28.4 | 15.9 | 12.5 | 480 | 90 | 4 |
| 0 | 24.5 | 30.9 | 17.9 | 13.0 | 1067 | 136 | 53 |
| 0 | 22.8 | 30.6 | 14.3 | 16.3 | 677 | 141 | 3 |
| 0 | 23.8 | 31.6 | 13.8 | 17.8 | 1192 | 275 | 3 |
| 0 | 27.0 | 33.1 | 22.1 | 11.0 | 2497 | 345 | 65 |
| 0 | 15.3 | 32.8 | 0.9 | 31.9 | 332 | 47 | 14 |
| 0 | 23.5 | 29.4 | 17.5 | 11.9 | 1835 | 192 | 111 |
| 0 | 19.9 | 28.6 | 9.8 | 18.8 | 1282 | 251 | 19 |
| 0 | 27.0 | 32.0 | 22.1 | 9.9 | 2093 | 388 | 15 |
| 0 | 4.1 | 13.6 | -7.1 | 20.7 | 612 | 131 | 7 |
| 0 | 26.4 | 32.7 | 21.8 | 10.9 | 2197 | 302 | 84 |
| 0 | 13.4 | 25.7 | 3.4 | 22.3 | 878 | 98 | 54 |
| 0 | 5.3 | 14.5 | -4.8 | 19.3 | 24 | 6 | 0 |
| 0 | 22.2 | 31.6 | 11.2 | 20.4 | 1325 | 177 | 49 |
| 0 | 21.8 | 30.5 | 12.4 | 18.1 | 1047 | 208 | 14 |
| 0 | 25.6 | 33.2 | 18.0 | 15.2 | 2271 | 356 | 26 |
| 0 | 26.6 | 33.1 | 20.9 | 12.2 | 2558 | 326 | 48 |
| 0 | 27.2 | 33.7 | 21.6 | 12.1 | 1515 | 259 | 16 |
| 0 | 18.5 | 25.3 | 11.2 | 14.1 | 1153 | 150 | 58 |
| 0 | 4.8 | 13.3 | -1.9 | 15.2 | 393 | 41 | 21 |
| 0 | 22.6 | 30.6 | 11.4 | 19.2 | 1195 | 221 | 16 |
| 0 | 18.8 | 27.9 | 8.7 | 19.2 | 1279 | 190 | 48 |
| 0 | 15.0 | 32.5 | 0.0 | 32.5 | 309 | 43 | 13 |
| 0 | 27.0 | 35.4 | 19.4 | 16.0 | 1604 | 389 | 8 |
| 0 | 26.6 | 32.4 | 21.1 | 11.3 | 2804 | 357 | 77 |
| 0 | 19.5 | 32.7 | 8.2 | 24.5 | 1266 | 141 | 67 |
| 0 | 26.4 | 32.8 | 20.6 | 12.2 | 2493 | 317 | 47 |
| 0 | 24.6 | 31.4 | 16.5 | 14.9 | 2511 | 336 | 73 |
| 0 | 20.6 | 28.9 | 9.3 | 19.6 | 1386 | 305 | 10 |
| 0 | 6.7 | 17.6 | -6.1 | 23.7 | 78 | 23 | 1 |
| 0 | 23.9 | 32.3 | 16.1 | 16.2 | 446 | 61 | 13 |
| 0 | 20.7 | 33.0 | 9.3 | 23.7 | 1061 | 129 | 38 |
| 0 | 25.5 | 32.4 | 17.5 | 14.9 | 1857 | 278 | 28 |
| 0 | 26.9 | 36.0 | 19.2 | 16.8 | 1862 | 410 | 2 |
| 0 | 22.3 | 34.7 | 8.7 | 26.0 | 721 | 113 | 8 |
| 0 | 24.6 | 31.8 | 15.8 | 16.0 | 1858 | 253 | 30 |
| 0 | 22.0 | 33.5 | 11.4 | 22.1 | 1299 | 173 | 47 |
| 0 | 25.1 | 33.2 | 15.0 | 18.2 | 1930 | 322 | 6 |
| 0 | 26.6 | 35.1 | 18.1 | 17.0 | 1740 | 268 | 4 |
| 0 | 25.3 | 32.5 | 18.5 | 14.0 | 1799 | 294 | 19 |
| 0 | 20.7 | 35.6 | 6.6 | 29.0 | 781 | 115 | 12 |
| 0 | 20.2 | 32.5 | 9.0 | 23.5 | 1650 | 179 | 101 |
| 0 | 25.6 | 31.3 | 19.6 | 11.7 | 2526 | 282 | 118 |
| 0 | 26.4 | 32.4 | 20.5 | 11.9 | 2954 | 372 | 81 |
| 0 | 26.1 | 32.8 | 21.3 | 11.5 | 2463 | 404 | 56 |
| 0 | 25.1 | 31.3 | 19.0 | 12.3 | 3562 | 480 | 119 |
| 0 | 26.8 | 33.2 | 20.9 | 12.3 | 1879 | 352 | 16 |
| 0 | 3.4 | 14.7 | -10.3 | 25.0 | 64 | 29 | 0 |
| 0 | 20.7 | 35.0 | 5.4 | 29.6 | 590 | 108 | 7 |
| 0 | 24.7 | 30.4 | 19.5 | 10.9 | 2290 | 332 | 80 |
| 0 | 26.3 | 32.5 | 20.9 | 11.6 | 2294 | 420 | 35 |
| 0 | 22.9 | 32.7 | 13.0 | 19.7 | 1397 | 198 | 37 |
| 0 | 25.5 | 34.5 | 16.6 | 17.9 | 2415 | 356 | 21 |
| 0 | 25.9 | 33.4 | 17.3 | 16.1 | 1134 | 203 | 29 |
| 0 | 16.3 | 27.6 | 1.3 | 26.3 | 670 | 169 | 3 |
| 0 | 15.0 | 32.3 | 0.9 | 31.4 | 611 | 81 | 17 |
| 0 | 25.1 | 31.9 | 20.0 | 11.9 | 2382 | 374 | 53 |
| 0 | 26.2 | 31.3 | 21.2 | 10.1 | 2863 | 335 | 175 |
| 0 | 25.7 | 33.3 | 16.2 | 17.1 | 1499 | 300 | 5 |
| 0 | 26.0 | 33.5 | 18.3 | 15.2 | 1570 | 290 | 21 |
| 0 | 24.8 | 33.9 | 14.4 | 19.5 | 759 | 126 | 14 |
| 0 | 4.6 | 12.1 | -5.4 | 17.5 | 872 | 133 | 14 |
| 0 | -2.5 | 10.9 | -14.1 | 25.0 | 350 | 75 | 14 |
| 0 | 25.1 | 31.7 | 18.6 | 13.1 | 943 | 167 | 8 |
| 0 | 25.8 | 31.3 | 20.6 | 10.7 | 3007 | 334 | 184 |
| 0 | 4.3 | 18.0 | -7.5 | 25.5 | 289 | 55 | 11 |
| 0 | 22.6 | 31.0 | 12.2 | 18.8 | 1637 | 274 | 12 |
| 0 | 25.2 | 31.2 | 19.3 | 11.9 | 2758 | 451 | 47 |
| 0 | 16.9 | 33.6 | -0.3 | 33.9 | 102 | 21 | 2 |
| 0 | 27.1 | 33.8 | 20.9 | 12.9 | 1157 | 194 | 8 |
| 0 | 22.6 | 30.1 | 12.8 | 17.3 | 1437 | 244 | 6 |
| 0 | 18.4 | 25.5 | 8.1 | 17.4 | 1579 | 298 | 17 |
| 0 | 16.0 | 23.1 | 9.2 | 13.9 | 2249 | 275 | 100 |
| 0 | 27.3 | 35.4 | 21.3 | 14.1 | 1684 | 297 | 5 |
| 0 | 25.6 | 33.8 | 17.0 | 16.8 | 2321 | 370 | 13 |
| 0 | 18.1 | 31.5 | 6.8 | 24.7 | 1374 | 144 | 88 |
| 0 | 25.1 | 32.0 | 19.8 | 12.2 | 2338 | 365 | 56 |
| 0 | 27.1 | 33.1 | 22.4 | 10.7 | 2184 | 327 | 61 |
| 0 | 16.2 | 33.1 | 1.8 | 31.3 | 642 | 89 | 17 |
| 0 | 26.0 | 34.4 | 17.6 | 16.8 | 2173 | 341 | 26 |
| 0 | 26.2 | 32.1 | 21.1 | 11.0 | 1843 | 324 | 31 |
| 0 | 17.9 | 29.0 | 4.0 | 25.0 | 731 | 173 | 4 |
| 0 | 25.1 | 34.3 | 14.7 | 19.6 | 1041 | 158 | 19 |
| 0 | 26.8 | 33.5 | 20.2 | 13.3 | 2224 | 310 | 50 |
| 0 | 18.7 | 29.2 | 9.6 | 19.6 | 1587 | 160 | 104 |
| 0 | 17.8 | 33.4 | -0.3 | 33.7 | 185 | 48 | 2 |
| 0 | 26.5 | 34.8 | 17.6 | 17.2 | 1483 | 244 | 2 |
| 0 | 6.6 | 21.8 | -5.0 | 26.8 | 223 | 38 | 7 |
| 0 | 25.6 | 32.2 | 19.4 | 12.8 | 1117 | 148 | 23 |
| 0 | 22.9 | 30.7 | 12.6 | 18.1 | 1302 | 248 | 11 |
| 0 | 23.5 | 31.3 | 14.1 | 17.2 | 1435 | 194 | 29 |
| 0 | 15.3 | 31.9 | 2.0 | 29.9 | 764 | 99 | 24 |
| 0 | 18.1 | 24.1 | 11.2 | 12.9 | 1133 | 167 | 27 |
| 0 | 21.5 | 28.2 | 15.3 | 12.9 | 1051 | 173 | 16 |
| 0 | 9.8 | 22.5 | -1.1 | 23.6 | 218 | 26 | 13 |
| 0 | 23.5 | 28.5 | 18.0 | 10.5 | 1654 | 235 | 46 |
| 0 | 16.8 | 33.0 | 0.6 | 32.4 | 142 | 26 | 4 |
| 0 | 18.9 | 32.6 | 6.2 | 26.4 | 938 | 144 | 26 |
| 0 | 24.6 | 31.8 | 17.2 | 14.6 | 1577 | 250 | 14 |
| 0 | 26.5 | 32.6 | 20.2 | 12.4 | 2430 | 263 | 115 |
| 0 | 8.3 | 23.6 | -2.8 | 26.4 | 1001 | 213 | 12 |
| 0 | 26.1 | 33.5 | 19.5 | 14.0 | 3482 | 417 | 198 |
| 0 | 18.9 | 28.9 | 11.7 | 17.2 | 19 | 3 | 0 |
| 0 | 25.7 | 32.3 | 18.6 | 13.7 | 2471 | 318 | 83 |
| 0 | 25.4 | 32.6 | 18.3 | 14.3 | 1447 | 315 | 9 |
| 0 | 24.6 | 34.0 | 13.4 | 20.6 | 1850 | 330 | 2 |
| 0 | 26.1 | 32.3 | 20.2 | 12.1 | 1074 | 178 | 16 |
| 0 | 11.2 | 24.5 | 0.4 | 24.1 | 179 | 26 | 10 |
| 0 | 25.5 | 31.7 | 19.7 | 12.0 | 2064 | 382 | 30 |
| 0 | 25.7 | 31.6 | 19.2 | 12.4 | 2456 | 270 | 79 |
| 0 | 24.5 | 32.6 | 16.6 | 16.0 | 1218 | 219 | 5 |
| 0 | 26.4 | 32.1 | 21.4 | 10.7 | 2510 | 334 | 82 |
| 0 | 24.2 | 31.8 | 15.8 | 16.0 | 579 | 136 | 3 |
| 0 | 27.4 | 34.1 | 21.2 | 12.9 | 727 | 195 | 2 |
| 0 | 12.0 | 17.3 | 6.7 | 10.6 | 1070 | 139 | 40 |
| 0 | 25.7 | 31.5 | 19.0 | 12.5 | 2469 | 269 | 79 |
| 0 | 9.6 | 22.2 | 1.7 | 20.5 | 1458 | 271 | 28 |
| 0 | 21.0 | 28.1 | 15.3 | 12.8 | 1883 | 233 | 117 |
| 0 | 25.2 | 34.0 | 14.7 | 19.3 | 1673 | 292 | 2 |
| 0 | 26.7 | 31.6 | 22.3 | 9.3 | 1913 | 285 | 11 |
| 0 | 25.0 | 33.0 | 17.1 | 15.9 | 2027 | 315 | 16 |
| 0 | 25.8 | 32.0 | 20.5 | 11.5 | 2728 | 325 | 70 |
| 0 | 4.7 | 15.6 | -5.2 | 20.8 | 250 | 26 | 16 |
| 0 | 27.0 | 33.1 | 21.9 | 11.2 | 2342 | 358 | 50 |
| 0 | 21.7 | 32.1 | 11.4 | 20.7 | 1451 | 165 | 73 |
| 0 | 25.6 | 31.3 | 19.6 | 11.7 | 2487 | 251 | 166 |
| 0 | 5.8 | 13.6 | -0.5 | 14.1 | 1585 | 164 | 120 |
| 0 | 25.2 | 33.1 | 14.7 | 18.4 | 1837 | 341 | 9 |
| 0 | 26.2 | 31.6 | 20.5 | 11.1 | 2942 | 328 | 171 |
| 0 | 19.7 | 27.9 | 9.6 | 18.3 | 1512 | 328 | 14 |
| 0 | 27.5 | 35.0 | 21.0 | 14.0 | 1546 | 286 | 8 |
| 0 | 20.8 | 34.8 | 5.0 | 29.8 | 433 | 90 | 4 |
| 0 | 23.9 | 30.9 | 14.9 | 16.0 | 1252 | 176 | 24 |
| 0 | 18.5 | 28.7 | 8.5 | 20.2 | 3 | 1 | 0 |
| 0 | 25.5 | 33.8 | 15.8 | 18.0 | 1581 | 283 | 2 |
| 0 | 24.2 | 32.8 | 13.7 | 19.1 | 1453 | 257 | 14 |
| 0 | 25.9 | 31.4 | 20.0 | 11.4 | 2545 | 273 | 142 |
| 0 | 26.6 | 32.2 | 21.9 | 10.3 | 2586 | 344 | 89 |
| 0 | 22.2 | 31.3 | 10.5 | 20.8 | 1795 | 329 | 5 |
| 0 | 26.4 | 34.8 | 17.9 | 16.9 | 1839 | 290 | 6 |
| 0 | 26.7 | 33.0 | 21.3 | 11.7 | 2498 | 404 | 58 |
| 0 | 23.2 | 30.0 | 16.8 | 13.2 | 667 | 87 | 26 |
| 0 | 20.4 | 26.1 | 14.2 | 11.9 | 2606 | 495 | 23 |
| 0 | 19.9 | 32.7 | 5.2 | 27.5 | 915 | 137 | 30 |
| 0 | 27.9 | 35.5 | 22.4 | 13.1 | 2813 | 442 | 49 |
| 0 | 26.3 | 32.8 | 20.1 | 12.7 | 2945 | 382 | 63 |
| 0 | 25.9 | 30.5 | 22.0 | 8.5 | 4328 | 536 | 280 |
| 0 | 23.6 | 30.2 | 14.3 | 15.9 | 1405 | 204 | 15 |
| 0 | 25.4 | 32.3 | 19.2 | 13.1 | 820 | 196 | 7 |
| 0 | 21.7 | 29.2 | 12.2 | 17.0 | 1537 | 272 | 6 |
| 0 | 22.6 | 30.2 | 14.7 | 15.5 | 1063 | 159 | 12 |
| 0 | 13.0 | 25.3 | 2.2 | 23.1 | 190 | 25 | 9 |
| 0 | 26.8 | 32.0 | 21.8 | 10.2 | 2498 | 434 | 23 |
| 0 | 13.1 | 22.5 | 4.4 | 18.1 | 126 | 42 | 0 |
| 0 | 22.7 | 30.4 | 13.4 | 17.0 | 1288 | 272 | 4 |
| 0 | 26.3 | 32.8 | 19.9 | 12.9 | 2418 | 332 | 44 |
| 0 | 15.7 | 28.9 | 2.3 | 26.6 | 613 | 98 | 7 |
| 0 | 26.0 | 31.9 | 20.1 | 11.8 | 2515 | 321 | 65 |
| 0 | 16.1 | 33.3 | 1.2 | 32.1 | 583 | 80 | 14 |
| 0 | 20.3 | 29.0 | 9.3 | 19.7 | 1241 | 208 | 27 |
| 0 | 23.0 | 34.8 | 10.9 | 23.9 | 967 | 116 | 18 |
| 0 | 21.1 | 29.1 | 11.2 | 17.9 | 2094 | 320 | 55 |
| 0 | 5.6 | 13.8 | -5.2 | 19.0 | 803 | 140 | 10 |
| 0 | 26.4 | 31.8 | 20.9 | 10.9 | 2748 | 306 | 150 |
| 0 | 25.4 | 33.4 | 14.6 | 18.8 | 1567 | 312 | 5 |
| 0 | 19.2 | 27.0 | 8.6 | 18.4 | 1640 | 299 | 24 |
| 0 | 28.2 | 34.7 | 22.9 | 11.8 | 3308 | 501 | 41 |
| 0 | 26.2 | 32.8 | 20.1 | 12.7 | 2876 | 376 | 55 |
| 0 | 17.3 | 30.4 | 6.3 | 24.1 | 1042 | 115 | 65 |
| 0 | 24.2 | 32.1 | 12.9 | 19.2 | 1273 | 247 | 7 |
| 0 | 25.7 | 32.2 | 20.2 | 12.0 | 1961 | 292 | 50 |
| 0 | 21.6 | 28.2 | 13.8 | 14.4 | 1489 | 263 | 7 |
| 0 | 24.6 | 33.1 | 15.0 | 18.1 | 860 | 149 | 27 |
| 0 | 25.3 | 32.2 | 20.0 | 12.2 | 2551 | 373 | 59 |
| 0 | 24.9 | 31.8 | 16.4 | 15.4 | 1827 | 262 | 21 |
| 0 | 17.6 | 28.5 | 2.4 | 26.1 | 660 | 130 | 2 |
| 0 | 18.2 | 27.8 | 7.7 | 20.1 | 1720 | 199 | 91 |
| 0 | 16.6 | 25.9 | 6.0 | 19.9 | 1412 | 202 | 28 |
| 0 | 25.2 | 33.4 | 15.7 | 17.7 | 1418 | 238 | 13 |
| 0 | 16.1 | 31.4 | 3.1 | 28.3 | 841 | 107 | 27 |
| 0 | 25.2 | 31.9 | 17.1 | 14.8 | 1913 | 275 | 19 |
| 0 | 26.0 | 32.8 | 18.3 | 14.5 | 1885 | 277 | 35 |
| 0 | 26.6 | 32.2 | 21.6 | 10.6 | 2664 | 334 | 143 |
| 0 | 6.8 | 17.0 | -5.4 | 22.4 | 265 | 81 | 0 |
| 0 | 26.5 | 34.3 | 18.6 | 15.7 | 1672 | 262 | 14 |
| 0 | 19.5 | 33.2 | 7.5 | 25.7 | 999 | 133 | 34 |
| 0 | 10.2 | 21.6 | 0.4 | 21.2 | 220 | 28 | 11 |
| 0 | 25.5 | 30.7 | 20.2 | 10.5 | 3539 | 577 | 60 |
| 0 | 25.5 | 30.8 | 20.3 | 10.5 | 3308 | 333 | 202 |
| 0 | 27.5 | 34.7 | 22.0 | 12.7 | 2802 | 393 | 25 |
| 0 | 23.7 | 31.9 | 13.6 | 18.3 | 1595 | 264 | 14 |
| 0 | 27.2 | 33.5 | 22.2 | 11.3 | 2219 | 355 | 45 |
| 0 | 21.8 | 32.8 | 10.8 | 22.0 | 1573 | 181 | 70 |
| 0 | 26.6 | 32.3 | 21.4 | 10.9 | 2491 | 404 | 77 |
| 0 | 25.6 | 33.3 | 17.4 | 15.9 | 1726 | 321 | 4 |
| 0 | 21.4 | 30.2 | 10.5 | 19.7 | 1281 | 200 | 43 |
| 0 | 25.5 | 31.9 | 18.2 | 13.7 | 2147 | 302 | 40 |
| 0 | 20.9 | 29.1 | 11.2 | 17.9 | 1275 | 300 | 3 |
| 0 | 26.7 | 33.1 | 21.2 | 11.9 | 2336 | 340 | 77 |
| 0 | 19.8 | 32.8 | 8.6 | 24.2 | 1299 | 151 | 62 |
| 0 | 25.7 | 33.5 | 17.7 | 15.8 | 2240 | 351 | 18 |
| 0 | 27.6 | 34.1 | 21.8 | 12.3 | 1836 | 321 | 18 |
| 0 | 23.2 | 32.3 | 11.7 | 20.6 | 1045 | 218 | 4 |
| 0 | 25.9 | 34.0 | 16.8 | 17.2 | 1670 | 276 | 29 |
| 0 | 26.5 | 32.3 | 20.7 | 11.6 | 2146 | 238 | 105 |
| 0 | 24.8 | 33.2 | 16.6 | 16.6 | 1192 | 198 | 1 |
| 0 | 13.3 | 28.0 | 0.5 | 27.5 | 178 | 21 | 12 |
| 0 | 24.0 | 32.4 | 14.2 | 18.2 | 1492 | 259 | 12 |
| 0 | 14.8 | 23.7 | 6.7 | 17.0 | 66 | 19 | 0 |
| 0 | 22.9 | 30.6 | 11.8 | 18.8 | 1222 | 237 | 16 |
| 0 | 26.0 | 34.2 | 16.0 | 18.2 | 1334 | 223 | 16 |
| 0 | 26.4 | 34.4 | 18.4 | 16.0 | 1659 | 258 | 8 |
| 0 | 24.6 | 33.5 | 15.4 | 18.1 | 724 | 144 | 1 |
| 0 | 26.6 | 32.4 | 21.1 | 11.3 | 2797 | 356 | 76 |
| 0 | 23.2 | 31.6 | 12.8 | 18.8 | 1681 | 268 | 9 |
| 0 | 25.5 | 31.6 | 18.7 | 12.9 | 2464 | 317 | 58 |
| 0 | 21.7 | 30.1 | 10.8 | 19.3 | 1201 | 224 | 21 |
| 0 | 19.4 | 29.0 | 9.2 | 19.8 | 1454 | 216 | 28 |
| 0 | 26.6 | 32.1 | 21.7 | 10.4 | 2521 | 301 | 129 |
| 0 | 24.6 | 31.3 | 16.8 | 14.5 | 3068 | 431 | 100 |
| 0 | 26.3 | 33.8 | 17.9 | 15.9 | 1640 | 259 | 28 |
| 0 | 4.8 | 13.2 | -2.0 | 15.2 | 1867 | 214 | 110 |
| 0 | 26.2 | 33.4 | 18.9 | 14.5 | 2418 | 331 | 34 |
| 0 | 26.6 | 32.2 | 21.8 | 10.4 | 2518 | 317 | 103 |
| 0 | 25.0 | 30.2 | 20.2 | 10.0 | 1704 | 286 | 35 |
| 0 | 22.7 | 31.5 | 13.1 | 18.4 | 1874 | 318 | 8 |
| 0 | 25.4 | 31.8 | 19.7 | 12.1 | 2352 | 346 | 53 |
| 0 | 25.1 | 31.6 | 20.4 | 11.2 | 2435 | 343 | 68 |
| 0 | 20.3 | 28.2 | 11.0 | 17.2 | 1097 | 240 | 4 |
| 0 | 24.5 | 32.9 | 16.2 | 16.7 | 2090 | 338 | 20 |
| 0 | 25.0 | 31.7 | 16.9 | 14.8 | 2081 | 298 | 36 |
| 0 | 3.7 | 14.7 | -9.4 | 24.1 | 516 | 134 | 1 |
| 0 | 25.6 | 31.9 | 18.4 | 13.5 | 2452 | 321 | 51 |
| 0 | 12.7 | 26.9 | 0.3 | 26.6 | 177 | 22 | 11 |
| 0 | 23.7 | 31.5 | 13.9 | 17.6 | 1414 | 187 | 35 |
| 0 | 7.3 | 21.0 | -3.5 | 24.5 | 172 | 27 | 6 |
| 0 | 20.5 | 34.7 | 5.0 | 29.7 | 564 | 111 | 6 |
| 0 | 25.3 | 35.6 | 15.1 | 20.5 | 2378 | 402 | 4 |
| 0 | 26.0 | 33.5 | 18.9 | 14.6 | 1827 | 281 | 20 |
| 0 | 21.5 | 33.6 | 10.6 | 23.0 | 1552 | 161 | 79 |
| 0 | 20.8 | 33.1 | 9.6 | 23.5 | 1139 | 143 | 42 |
| 0 | 15.0 | 32.0 | 1.1 | 30.9 | 332 | 44 | 14 |
| 0 | 20.9 | 35.2 | 7.5 | 27.7 | 963 | 137 | 17 |
| 0 | 19.4 | 33.2 | 6.3 | 26.9 | 928 | 137 | 22 |
| 0 | 27.8 | 35.0 | 21.2 | 13.8 | 1126 | 201 | 14 |
| 0 | 24.0 | 31.3 | 17.3 | 14.0 | 718 | 188 | 1 |
| 0 | 26.8 | 32.4 | 21.5 | 10.9 | 2266 | 317 | 96 |
| 0 | 5.0 | 17.2 | -4.4 | 21.6 | 1024 | 159 | 38 |
| 0 | 18.4 | 24.2 | 12.1 | 12.1 | 2825 | 379 | 68 |
| 0 | 25.8 | 34.5 | 15.8 | 18.7 | 1057 | 162 | 27 |
| 0 | 26.0 | 32.3 | 21.5 | 10.8 | 2450 | 332 | 77 |
| 0 | 7.4 | 17.6 | -6.6 | 24.2 | 717 | 147 | 3 |
| 0 | 21.3 | 33.5 | 6.6 | 26.9 | 613 | 123 | 1 |
| 0 | 26.1 | 33.4 | 18.1 | 15.3 | 1756 | 264 | 32 |
| 0 | 22.9 | 32.4 | 10.9 | 21.5 | 1765 | 326 | 7 |
| 0 | 25.4 | 33.1 | 15.7 | 17.4 | 1341 | 231 | 29 |
| 0 | 15.9 | 32.7 | 2.0 | 30.7 | 656 | 92 | 19 |
| 0 | 25.8 | 33.3 | 16.4 | 16.9 | 1276 | 225 | 29 |
| 0 | 26.4 | 32.1 | 21.0 | 11.1 | 2235 | 216 | 137 |
| 0 | 25.0 | 32.8 | 15.2 | 17.6 | 1483 | 250 | 27 |
| 0 | 23.4 | 32.7 | 12.3 | 20.4 | 1142 | 188 | 20 |
| 0 | 26.5 | 34.7 | 18.5 | 16.2 | 1118 | 207 | 4 |
| 0 | 20.1 | 28.3 | 12.2 | 16.1 | 1582 | 209 | 77 |
| 0 | 25.8 | 34.3 | 17.5 | 16.8 | 2171 | 344 | 20 |
| 0 | 25.9 | 31.4 | 20.7 | 10.7 | 2907 | 326 | 166 |
| 0 | 24.8 | 31.5 | 19.9 | 11.6 | 2473 | 381 | 59 |
| 0 | 25.5 | 31.6 | 20.0 | 11.6 | 1476 | 286 | 19 |
| 0 | 25.9 | 31.4 | 20.9 | 10.5 | 2916 | 432 | 102 |
| 0 | 25.9 | 32.6 | 21.1 | 11.5 | 2388 | 402 | 53 |
| 0 | 24.4 | 30.2 | 19.0 | 11.2 | 2871 | 377 | 159 |
| 0 | 24.0 | 30.0 | 17.5 | 12.5 | 941 | 131 | 49 |
| 0 | 26.2 | 33.5 | 21.1 | 12.4 | 2205 | 373 | 77 |
| 0 | 23.2 | 31.0 | 12.8 | 18.2 | 1223 | 192 | 25 |
| 0 | 23.2 | 30.6 | 15.8 | 14.8 | 892 | 216 | 5 |
| 0 | 23.8 | 32.9 | 14.6 | 18.3 | 1773 | 274 | 10 |
| 0 | 6.3 | 17.7 | -8.2 | 25.9 | 337 | 108 | 1 |
| 0 | 22.2 | 30.2 | 11.0 | 19.2 | 1333 | 274 | 9 |
| 0 | 18.5 | 31.4 | 7.7 | 23.7 | 1425 | 142 | 100 |
| 0 | 23.7 | 32.9 | 13.4 | 19.5 | 1404 | 186 | 46 |
| 0 | 11.0 | 21.2 | 1.6 | 19.6 | 97 | 32 | 0 |
| 0 | 25.7 | 31.5 | 19.6 | 11.9 | 2441 | 265 | 105 |
| 0 | 26.8 | 33.5 | 21.2 | 12.3 | 2684 | 346 | 54 |
| 0 | 21.2 | 29.8 | 10.1 | 19.7 | 1212 | 212 | 25 |
| 0 | 25.6 | 31.7 | 19.4 | 12.3 | 3520 | 517 | 51 |
| 0 | 26.5 | 33.5 | 19.3 | 14.2 | 1803 | 232 | 60 |
| 0 | 24.6 | 32.2 | 15.2 | 17.0 | 1433 | 240 | 31 |
| 0 | 25.4 | 31.8 | 18.0 | 13.8 | 2201 | 297 | 39 |
| 0 | 25.0 | 32.8 | 15.3 | 17.5 | 1438 | 244 | 33 |
| 0 | 19.0 | 32.7 | 6.5 | 26.2 | 948 | 145 | 30 |
| 0 | 25.7 | 31.0 | 20.6 | 10.4 | 3499 | 386 | 223 |
| 0 | 19.1 | 26.1 | 11.3 | 14.8 | 970 | 139 | 36 |
| 0 | 18.3 | 28.5 | 9.2 | 19.3 | 1664 | 180 | 123 |
| 0 | 22.0 | 29.8 | 15.2 | 14.6 | 2876 | 492 | 29 |
| 0 | 19.0 | 26.8 | 12.5 | 14.3 | 15 | 4 | 0 |
| 0 | 23.6 | 32.5 | 13.2 | 19.3 | 1369 | 178 | 44 |
| 0 | 23.7 | 31.8 | 15.1 | 16.7 | 1152 | 255 | 0 |
| 0 | 23.2 | 29.2 | 16.8 | 12.4 | 2306 | 457 | 13 |
| 0 | 25.6 | 33.5 | 17.5 | 16.0 | 2493 | 385 | 16 |
| 0 | 25.9 | 33.6 | 16.3 | 17.3 | 1536 | 278 | 4 |
| 0 | 5.3 | 18.0 | -10.2 | 28.2 | 80 | 31 | 0 |
| 0 | 25.7 | 31.2 | 20.3 | 10.9 | 2879 | 318 | 159 |
| 0 | 24.4 | 32.3 | 16.6 | 15.7 | 2015 | 308 | 21 |
| 0 | 20.6 | 29.5 | 10.0 | 19.5 | 1242 | 193 | 33 |
| 0 | 22.5 | 30.5 | 11.4 | 19.1 | 1346 | 289 | 10 |
| 0 | 25.0 | 35.0 | 14.3 | 20.7 | 1915 | 319 | 1 |
| 0 | 15.7 | 24.8 | 6.5 | 18.3 | 5 | 2 | 0 |
| 0 | 26.5 | 34.5 | 17.9 | 16.6 | 1558 | 274 | 2 |
| 0 | 24.7 | 30.4 | 19.6 | 10.8 | 2643 | 548 | 34 |
| 0 | 24.4 | 32.3 | 15.1 | 17.2 | 948 | 167 | 30 |
| 0 | 26.2 | 34.4 | 16.5 | 17.9 | 1241 | 209 | 18 |
| 0 | 24.3 | 30.6 | 18.3 | 12.3 | 1360 | 230 | 30 |
| 0 | 26.1 | 31.1 | 20.9 | 10.2 | 2532 | 301 | 146 |
| 0 | 8.8 | 19.8 | -5.9 | 25.7 | 275 | 92 | 1 |
| 0 | 25.8 | 32.2 | 20.7 | 11.5 | 3243 | 396 | 118 |
| 0 | 26.1 | 33.9 | 18.5 | 15.4 | 1704 | 263 | 13 |
| 0 | 21.5 | 34.2 | 7.2 | 27.0 | 654 | 133 | 2 |
| 0 | 23.0 | 32.5 | 11.0 | 21.5 | 1752 | 323 | 7 |
| 0 | 25.6 | 30.7 | 20.4 | 10.3 | 3137 | 326 | 178 |
| 0 | 6.5 | 14.2 | -3.2 | 17.4 | 1316 | 188 | 26 |
| 0 | 21.2 | 36.3 | 6.5 | 29.8 | 600 | 104 | 6 |
| 0 | 16.9 | 25.9 | 7.1 | 18.8 | 1717 | 216 | 98 |
| 0 | 27.1 | 32.7 | 22.1 | 10.6 | 2175 | 300 | 78 |
| 0 | 22.1 | 30.0 | 15.2 | 14.8 | 2517 | 476 | 13 |
| 0 | 24.7 | 33.1 | 14.9 | 18.2 | 1258 | 204 | 27 |
| 0 | 27.7 | 33.3 | 22.2 | 11.1 | 2478 | 346 | 70 |
| 0 | 26.6 | 33.0 | 20.5 | 12.5 | 2080 | 419 | 18 |
| 0 | 26.3 | 32.2 | 20.5 | 11.7 | 2597 | 299 | 128 |
| 0 | 25.5 | 35.5 | 14.9 | 20.6 | 968 | 167 | 1 |
| 0 | 26.8 | 32.9 | 21.8 | 11.1 | 2277 | 396 | 87 |
| 0 | 26.2 | 33.3 | 19.0 | 14.3 | 2515 | 368 | 25 |
| 0 | 23.3 | 32.1 | 12.2 | 19.9 | 1660 | 293 | 11 |
| 0 | 24.2 | 32.9 | 13.3 | 19.6 | 2000 | 360 | 4 |
| 0 | 25.9 | 32.7 | 18.6 | 14.1 | 1886 | 257 | 54 |
| 0 | 24.9 | 33.5 | 16.2 | 17.3 | 2043 | 312 | 12 |
| 0 | 16.7 | 27.8 | 5.0 | 22.8 | 2049 | 207 | 128 |
| 0 | 18.2 | 25.9 | 8.7 | 17.2 | 609 | 121 | 7 |
| 0 | 25.0 | 35.6 | 13.8 | 21.8 | 2229 | 371 | 2 |
| 0 | 28.0 | 35.9 | 22.5 | 13.4 | 2098 | 396 | 5 |
| 0 | 26.3 | 33.4 | 20.1 | 13.3 | 3522 | 470 | 160 |
| 0 | 24.6 | 34.2 | 15.2 | 19.0 | 2427 | 379 | 14 |
| 0 | 24.2 | 32.1 | 16.5 | 15.6 | 1539 | 292 | 2 |
| 0 | 19.8 | 28.7 | 9.3 | 19.4 | 1219 | 189 | 32 |
| 0 | 27.3 | 33.2 | 22.8 | 10.4 | 1998 | 365 | 41 |
| 0 | 25.1 | 30.7 | 18.8 | 11.9 | 1913 | 305 | 41 |
| 0 | 24.2 | 34.6 | 12.3 | 22.3 | 922 | 166 | 0 |
| 0 | 26.0 | 33.5 | 17.9 | 15.6 | 1721 | 288 | 45 |
| 0 | 25.7 | 30.7 | 20.7 | 10.0 | 3011 | 329 | 185 |
| 0 | 26.7 | 35.1 | 18.6 | 16.5 | 751 | 151 | 0 |
| 0 | 27.2 | 32.8 | 21.8 | 11.0 | 1793 | 303 | 67 |
| 0 | 19.9 | 34.3 | 5.2 | 29.1 | 493 | 95 | 7 |
| 0 | 20.5 | 35.5 | 5.7 | 29.8 | 670 | 110 | 9 |
| 0 | 26.4 | 32.5 | 20.6 | 11.9 | 2707 | 388 | 53 |
| 0 | 6.7 | 12.3 | 1.6 | 10.7 | 6263 | 631 | 344 |
| 0 | 27.0 | 33.4 | 22.2 | 11.2 | 2462 | 376 | 89 |
| 0 | 18.2 | 28.6 | 9.6 | 19.0 | 1428 | 136 | 100 |
| 0 | 27.7 | 35.5 | 21.9 | 13.6 | 1765 | 364 | 1 |
| 0 | 27.1 | 33.3 | 22.4 | 10.9 | 2375 | 413 | 51 |
| 0 | 27.1 | 32.0 | 22.9 | 9.1 | 2056 | 412 | 6 |
| 0 | 23.9 | 33.0 | 13.2 | 19.8 | 1050 | 180 | 19 |
| 0 | 1.6 | 11.7 | -11.1 | 22.8 | 475 | 122 | 1 |
| 0 | 26.1 | 33.0 | 18.6 | 14.4 | 1879 | 272 | 18 |
| 0 | 24.7 | 32.7 | 17.3 | 15.4 | 814 | 184 | 1 |
| 0 | 15.5 | 32.7 | 0.9 | 31.8 | 287 | 37 | 18 |
| 0 | 24.5 | 32.9 | 13.8 | 19.1 | 1485 | 259 | 22 |
| 0 | 23.1 | 30.5 | 15.0 | 15.5 | 1029 | 173 | 26 |
| 0 | 27.2 | 32.6 | 22.4 | 10.2 | 1711 | 359 | 6 |
| 0 | 15.3 | 31.4 | 1.7 | 29.7 | 255 | 29 | 15 |
| 0 | 27.1 | 34.2 | 20.4 | 13.8 | 1656 | 333 | 19 |
| 0 | 20.1 | 28.2 | 13.5 | 14.7 | 6 | 2 | 0 |
| 0 | 27.0 | 32.6 | 22.8 | 9.8 | 2937 | 483 | 47 |
| 0 | 23.9 | 34.7 | 14.1 | 20.6 | 2448 | 419 | 10 |
| 0 | 26.2 | 32.1 | 20.5 | 11.6 | 1808 | 299 | 55 |
| 0 | 23.4 | 34.7 | 12.1 | 22.6 | 965 | 130 | 26 |
| 0 | 25.4 | 32.1 | 17.6 | 14.5 | 2016 | 303 | 33 |
| 0 | 25.5 | 34.9 | 15.0 | 19.9 | 927 | 133 | 21 |
| 0 | 16.4 | 32.3 | 0.1 | 32.2 | 204 | 46 | 2 |
| 0 | 26.6 | 32.1 | 21.5 | 10.6 | 2761 | 331 | 154 |
| 0 | 20.7 | 27.9 | 11.0 | 16.9 | 1595 | 313 | 13 |
| 0 | 20.7 | 28.8 | 11.0 | 17.8 | 938 | 214 | 4 |
¿Que hacemos primero?
set.seed(2018) Index1 <- createDataPartition(sp2$presence, list = FALSE) Train1 <- sp2[Index1, ] Test1 <- sp2[-Index1, ] nrow(Train1 %>% filter(presence == 1))
## [1] 70
nrow(Test1 %>% filter(presence == 1))
## [1] 90
Luego
fitControl <- trainControl(method = "repeatedcv", number = 10, repeats = 10) set.seed(2018) Model <- train(presence ~ ., data = Train1, method = "rpart", trControl = fitControl) caret::postResample(pred = predict(Model, Train1), obs = Train1$presence)
## RMSE Rsquared MAE ## 0.15076014 0.78582891 0.04545724
caret::postResample(pred = predict(Model, Test1), obs = Test1$presence)
## RMSE Rsquared MAE ## 0.20198494 0.69140834 0.06515482
Veamos el modelo
Más del modelo
¿Hagamos un mapa?
library(raster) Map <- predict(SA, Model)
Mapas
Probemos más algoritmos
set.seed(2020) Model2 <- train(presence ~ ., data = Train1, method = "gbm", trControl = fitControl) set.seed(2020) Model3 <- train(presence ~ ., data = Train1, method = "rf", trControl = fitControl)
Como rinden
caret::postResample(pred = predict(Model, Test1), obs = Test1$presence)
## RMSE Rsquared MAE ## 0.20198494 0.69140834 0.06515482
caret::postResample(pred = predict(Model2, Test1), obs = Test1$presence)
## RMSE Rsquared MAE ## 0.13878937 0.85740602 0.04794292
caret::postResample(pred = predict(Model3, Test1), obs = Test1$presence)
## RMSE Rsquared MAE ## 0.13478997 0.86460934 0.03865672
Comparar entre modelos
Comp <- resamples(list(Rpart = Model, GBM = Model2, RF = Model3)) Difs <- diff(Comp)
Más comparaciones
densityplot(Difs, metric = "Rsquared", auto.key = TRUE, pch = "|")
Mas comparaciones
bwplot(Difs, metric = "Rsquared")
Mas mapas
Map2 <- predict(SA, Model2) Map3 <- predict(SA, Model3)
Mas mapas
Sigan probando más algoritmos
Se puede con GLM binomial tambien
FitGlob <- glm(presence ~ ., family = binomial, data = sp2) library(MuMIn) smat <- abs(cor(sp2[, -1])) <= 0.7 smat[!lower.tri(smat)] <- NA K = floor(nrow(sp2)/10) options(na.action = "na.fail") Selected <- dredge(FitGlob, subset = smat, m.lim = c(0, K))
Se puede con GLM binomial tambien
| (Intercept) | PPAnual | PPMesHum | PPMesSeco | TempMedia | TempMesCalido | TempMesFrio | TempRangoAnual | df | logLik | AICc | delta | weight | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 76 | 7.010 | -0.004 | 0.056 | NA | -0.257 | NA | NA | -0.192 | 5 | -169.152 | 348.356 | 0.000 | 9.995286e-01 |
| 87 | 6.547 | NA | 0.025 | -0.024 | NA | -0.232 | NA | -0.053 | 5 | -177.723 | 365.498 | 17.142 | 1.894341e-04 |
| 23 | 5.589 | NA | 0.027 | -0.024 | NA | -0.243 | NA | NA | 4 | -178.758 | 365.550 | 17.194 | 1.845491e-04 |
| 84 | 6.790 | -0.005 | 0.062 | NA | NA | -0.229 | NA | -0.073 | 5 | -178.775 | 367.602 | 19.246 | 6.614116e-05 |
| 20 | 5.452 | -0.005 | 0.064 | NA | NA | -0.243 | NA | NA | 4 | -180.696 | 369.426 | 21.070 | 2.657595e-05 |
| 74 | 8.048 | -0.002 | NA | NA | -0.295 | NA | NA | -0.231 | 4 | -183.025 | 374.084 | 25.728 | 2.588215e-06 |
| 12 | 2.854 | -0.004 | 0.064 | NA | -0.280 | NA | NA | NA | 4 | -183.432 | 374.898 | 26.542 | 1.722834e-06 |
| 85 | 7.650 | NA | NA | -0.017 | NA | -0.241 | NA | -0.092 | 4 | -184.972 | 377.980 | 29.624 | 3.690453e-07 |
| 21 | 5.952 | NA | NA | -0.015 | NA | -0.257 | NA | NA | 3 | -188.641 | 383.302 | 34.946 | 2.577891e-08 |
| 75 | 6.040 | NA | -0.008 | NA | -0.333 | NA | NA | -0.157 | 4 | -197.941 | 403.916 | 55.560 | 8.611416e-13 |
| 73 | 5.041 | NA | NA | NA | -0.330 | NA | NA | -0.121 | 3 | -199.734 | 405.489 | 57.133 | 3.922646e-13 |
| 82 | 7.846 | -0.002 | NA | NA | NA | -0.268 | NA | -0.093 | 4 | -199.018 | 406.071 | 57.716 | 2.930934e-13 |
| 18 | 5.939 | -0.001 | NA | NA | NA | -0.278 | NA | NA | 3 | -202.418 | 410.857 | 62.501 | 2.677905e-14 |
| 10 | 2.817 | -0.001 | NA | NA | -0.307 | NA | NA | NA | 3 | -204.386 | 414.792 | 66.436 | 3.744178e-15 |
| 9 | 2.519 | NA | NA | NA | -0.323 | NA | NA | NA | 2 | -208.132 | 420.274 | 71.918 | 2.415046e-16 |
| 11 | 2.468 | NA | 0.002 | NA | -0.323 | NA | NA | NA | 3 | -208.020 | 422.061 | 73.705 | 9.883405e-17 |
| 19 | 5.884 | NA | -0.007 | NA | NA | -0.313 | NA | NA | 3 | -217.442 | 440.905 | 92.549 | 7.999741e-21 |
| 17 | 5.638 | NA | NA | NA | NA | -0.311 | NA | NA | 2 | -219.195 | 442.400 | 94.044 | 3.787261e-21 |
| 81 | 4.874 | NA | NA | NA | NA | -0.310 | NA | 0.038 | 3 | -218.326 | 442.672 | 94.316 | 3.306253e-21 |
| 97 | 4.874 | NA | NA | NA | NA | NA | -0.310 | -0.272 | 3 | -218.326 | 442.672 | 94.316 | 3.306253e-21 |
| 83 | 5.556 | NA | -0.006 | NA | NA | -0.312 | NA | 0.015 | 4 | -217.348 | 442.730 | 94.374 | 3.211549e-21 |
| 99 | 5.556 | NA | -0.006 | NA | NA | NA | -0.312 | -0.298 | 4 | -217.348 | 442.730 | 94.374 | 3.211549e-21 |
| 68 | 4.684 | -0.007 | 0.087 | NA | NA | NA | NA | -0.171 | 4 | -237.073 | 482.180 | 133.824 | 8.715860e-30 |
| 71 | 4.588 | NA | 0.031 | -0.036 | NA | NA | NA | -0.161 | 4 | -238.559 | 485.152 | 136.796 | 1.972245e-30 |
| 35 | -1.033 | NA | 0.010 | NA | NA | NA | -0.260 | NA | 3 | -258.723 | 523.467 | 175.111 | 9.439542e-39 |
| 69 | 5.250 | NA | NA | -0.027 | NA | NA | NA | -0.185 | 3 | -259.255 | 524.531 | 176.175 | 5.545591e-39 |
| 7 | 0.875 | NA | 0.037 | -0.034 | NA | NA | NA | NA | 3 | -260.103 | 526.227 | 177.871 | 2.374954e-39 |
| 4 | 0.751 | -0.007 | 0.086 | NA | NA | NA | NA | NA | 3 | -260.504 | 527.028 | 178.672 | 1.590976e-39 |
| 33 | -0.721 | NA | NA | NA | NA | NA | -0.245 | NA | 2 | -263.905 | 531.820 | 183.464 | 1.448777e-40 |
| 5 | 0.951 | NA | NA | -0.021 | NA | NA | NA | NA | 2 | -292.561 | 589.133 | 240.777 | 5.197630e-53 |
| 66 | 4.059 | -0.003 | NA | NA | NA | NA | NA | -0.153 | 3 | -317.702 | 641.425 | 293.069 | 2.293973e-64 |
| 2 | 0.425 | -0.002 | NA | NA | NA | NA | NA | NA | 2 | -343.323 | 690.657 | 342.301 | 4.677462e-75 |
| 65 | -2.909 | NA | NA | NA | NA | NA | NA | 0.059 | 2 | -457.796 | 919.602 | 571.246 | 9.020982e-125 |
| 67 | -2.749 | NA | -0.002 | NA | NA | NA | NA | 0.054 | 3 | -457.499 | 921.020 | 572.664 | 4.440723e-125 |
| 3 | -1.656 | NA | -0.005 | NA | NA | NA | NA | NA | 2 | -462.680 | 929.370 | 581.014 | 6.826821e-127 |
| 1 | -1.833 | NA | NA | NA | NA | NA | NA | NA | 1 | -465.380 | 932.764 | 584.408 | 1.250805e-127 |
GLM
best <- get.models(Selected, subset = delta < 2) best <- best[[1]] library(raster) MapLM <- predict(SA, best, type = "response")